7.Критерии оценивания в больших выборках
Полное описание вероятностных свойств оценки задается её выборочным распределением. Оценка параметра модели, полученная на основании выборочных данных, является СВ, а её конкретное значение является выборочным значением этой СВ. Математически доказали, что некоторые известные статистические оценки подчиняются законам распределения, формулы которых могут быть аналитически выведены и представлены в аналитической форме. Например, оценка математического ожидания при неизвестной дисперсии подчиняется распределению Стьюдента, а выборочная оценка дисперсии – распределению хи-квадрат.
На основании знаний выборочных распределений может быть решен вопрос о выборе наилучших оценок. Однако часто выборочное распределение оценки неизвестно, особенно при исследовании многомерных СВ. В этом случае иногда используют асимптотическое оценивание на основе выборочного нормального распределения, которое является предельным. Здесь применяется теореме Чебышева о том, что сумма СВ, распределенных по произвольным законам, с ростом размерности задачи стремятся к нормальному закону. В этом случае применяют ряд критериев, которые характеризуют различные предельные свойства оценок.
Критерии:
Состоятельность.
Оценка
является состоятельной, если при
она сходится по вероятности к своему
истинному значению. Сходимость по
вероятности означает, что существует
такое значение n, при
котором для любых сколь угодно малых
выполняется неравенство
- истинное значение оцениваемого
параметра. Состоятельность оценки
является асимптотическим, предельным
свойством оценки.
Несмещенность
оценки. Оценка
называется несмещенной, если её
математическое ожидание совпадает с
её истинным значением, т.е.
.
- величина смещения.
Несмещенность оценки является свойством, которое характерно для малых выборок. Если оценка состоятельна, то это не значит, что она не смещена. Если состоятельная оценка имеет конечное среднее, то она является асимптотически несмещенной. Понятие несмещенности никак не связано с понятием точности оценки, но связано с расположением истинной оценки на числовой оси.
Среднеквадратическое отклонение оценки.
Только для несмещенных оценок среднеквадратичное отклонение совпадает с дисперсией оценки. Наилучшую оценку рационально искать среди несмещенных оценок. Однако в этом случае дисперсия оценки может быть большой. Чаще в качестве критерия рассматривают минимум среднего квадратичного отклонения.
Эффективность оценки. Если оценка является несмещенной и состоятельной, то для неё можно определить границу дисперсии, которая не зависит от способа вычисления оценок.
Неравенство Крамера-Рао:
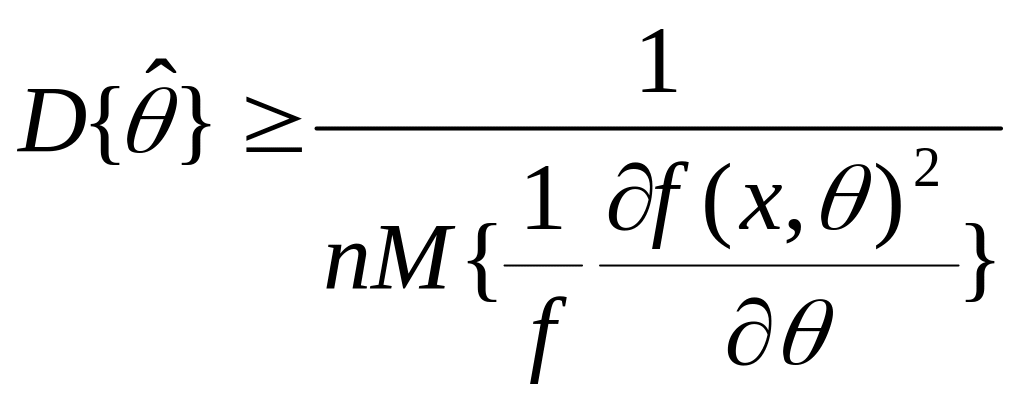
Это неравенство знаменито тем, что математическое ожидание в знаменателе есть количество информации Фишера. Оно эквивалентно количеству информации, содержащейся в одном наблюдении выборки. Чем выше объем выборки, тем меньше граница дисперсии. Оценка, для которой дисперсия совпадает с нижней границей в неравенстве Крамера-Рао, называется эффективной. Такие оценки обладают теоретически минимальной дисперсией
