16. Переходная и весовая функции

Переходная функция

Для получения переходной функции в качестве стандартного сигнала используется единичная функция времени (1.10). Такого рода воздействию соответствует, например, сброс или включение нагрузки в системах регулирования (отказ мотора в системе регулирования).

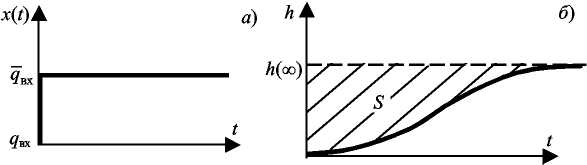
Рис. 2.4 Переходная характеристика:

а - ступенчатое воздействие; б - кривая разгона

Переходной функцией называется аналитическое выражение для решения линейного дифференциального уравнения (2.2) при входном сигнале x(t) = 1(t) и нулевых начальных условиях, т.е.

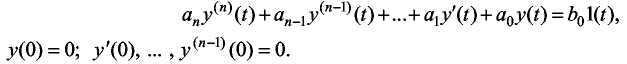(2.6)

Кривой разгона называется реакция объекта (системы) на единичное ступенчатое воздействие при нулевых начальных условиях.

На практике кривая разгона определяется экспериментальным путем и используется в качестве исходных данных для анализа и синтеза систем автоматического управления исследуемом объектом. Здесь следует ввести понятия прямой и обратной задач. Прямая задача (задача Коши) заключается в определении решения дифференциального уравнения с заданными начальными условиями. В обратной задаче требуется восстановить вид и коэффициенты дифференциального уравнения по известной интегральной кривой, например, переходной функции. Если предположить, что переходная функция описывается решением уравнения первого порядка

где , то определению подлежат k - коэффициент усиления и Т - постоянная времени.

В статике у'(t) = 0 и, следовательно, у(∞) = k x(∞), откуда коэффициент усиления так как x(∞) = 1; y(∞) = h(∞), то k = h(∞).

Для определения постоянной времени Т исходное уравнение интегрируется в пределах от 0 до ∞:

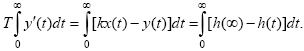
Правая часть последнего выражения есть не что иное, как площадь S под экспериментально снятой с кривой разгона (рис. 2.4б), тогда можно записать: Th(∞) = S, откуда

Весовая функция

Для получения весовой функции, ее также называют импульсной переходной функцией, в качестве стандартного сигнала используется δ-функция (1.11):

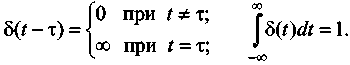
Таким образом, весовой функцией w(t) называется реакция системы на δ-функцию при нулевых начальных условиях.

На практике весовую функцию в отдельных случаях можно получить экспериментальным путем весьма приближенно (рис. 2.5). Считают, что на вход объекта подана δ-функция, если время действия импульса намного меньше времени переходного процесса.

Подаваемый на вход импульс представляет собой приближенную дельта-функцию, так как его площадь отлична от единицы и равна S. Поэтому для получения весовой функции экспериментально снятый переходный процесс нормируют путем деления его ординат на величину площади входного воздействия S.

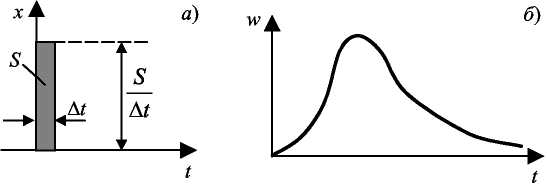
Рис. 2.5 Переходная характеристика:

а - δ-функция; б - весовая функция

Между временными характеристиками: переходной и весовой функциями существует взаимное однозначное соответствие, которое определяется следующим образом:

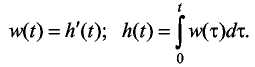
Весовую функцию можно получить и как решение дифференциального уравнения

17. Передаточная функция

Одной из основных характеристик объекта управления, используемой в теории автоматического управления, является передаточная функция, записываемая в терминах преобразования Лапласа.

Передаточной функцией объекта называется отношение преобразованного по Лапласу выхода объекта у(s) к преобразованному по Лапласу входу х(s) при нулевых начальных условиях.

Передаточная функция определяется только внутренними свойствами системы, является функцией комплексного переменного и обозначается:

(2.9)

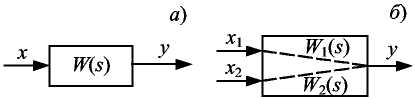
Рис. 2.6 Примеры различных объектов:

а — с одним входом и одним выходом; б — двумя входами и одним выходом;

в - двумя входами и двумя выходами

Передаточная функция характеризует динамику объекта только по определенному каналу, связывающему конкретный вход объекта и конкретный выход (рис. 2.6).

Если объект имеет несколько входов и выходов, то он характеризуется несколькими передаточными функциями, определить которые можно непосредственно, пользуясь определением (2.9).

Как и дифференциальное уравнение, передаточная функция полностью характеризует динамику линейного объекта. Если задано дифференциальное уравнение объекта, то для получения передаточной функции необходимо преобразовать дифференциальное уравнение по Лапласу и из полученного алгебраического уравнения найти отношение

В общем случае дифференциальное уравнение объекта представляется в виде

(2.10)

где a_n,…, a₀; b_m, …, b₀ — постоянные коэффициенты.

После преобразования по Лапласу при нулевых начальных условиях получают:

a_nsⁿy(s) + a_n−1s^n-1(s)+ ... + a₁sy(s) + a₀y(s) = b_ms^mx(s) + b_m−1s^m-1(s)+ ... +b₁sx(s) + b₀x(s), или

(a_nsⁿ + a_n-1s^n-1 + ... + a₁s + a₀) y(s) = (b_ms^m + b_m-1s^m-1 + ... + b₁s + b₀) x(s), и тогда

Если известна передаточная функция объекта, то изображение выхода объекта у(s) равно произведению передаточной функции на изображение входа x(s):

y(s) = W(s)x(s). (2.11)

Последняя запись есть не что иное, как общая форма записи решения дифференциального уравнения в операторной форме.

Таким образом, передаточная функция равна отношению двух полиномов:

где B(s) = b_ms^m + b_m-1s^m-1 ... + b₁s + b₀; A(s) = a_nsⁿ + a_n-1s^n-1 + a₁s + a₀ .

Для реальных физических объектов можно отметить как характерную особенность тот факт, что степень полинома В(s) всегда меньше или равна степени полинома A(s), т.е. m ≤ n, так что

Передаточная функция также взаимно однозначно связана с временными характеристиками.

Если имеется выражение для переходной функции, следовательно, входной сигнал x(t) = 1(t) или , выходной сигнал y(t) = h(t) или y(s) = h(s), и тогда передаточная функция равна

(2.12)

Из (2.12) может быть получено выражение для переходной функции через преобразование Лапласа:

(2.13)

Если известно выражение для весовой функции, то входной сигнал x(t) = δ(t) или x(s) = 1, выходной сигнал w(t) и, следовательно,

(2.14)

т.е. передаточная функция есть не что иное, как преобразование Лапласа от весовой функции.