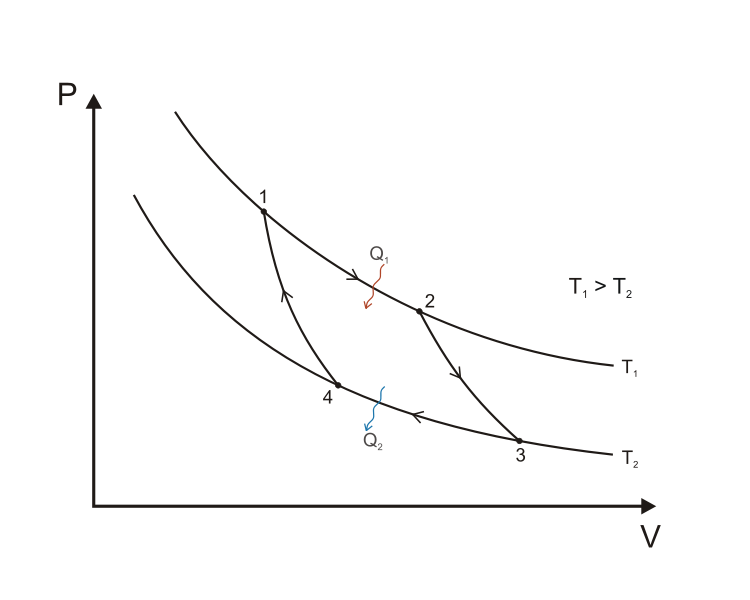
23. Цикл Карно и его кпд

Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.

Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.

Пусть тепловая машина состоит из нагревателя с температурой T_H, холодильника с температурой T_X и рабочего тела.

Цикл Карно состоит из четырёх стадий:

1. Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру T_H, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q_H. При этом объём рабочего тела увеличивается.

2. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

3. Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру T_X, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q_X.

4. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:

при δQ = 0.

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины, будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно.

24. 25. Реальные газы. Уравнение Ван-дер-Вальса.

Как мы видели, идеальный газ — это упрощенная модель реальных газов. В этой модели не учитываются объем молекул и силы взаимодействия между ними. Между тем молекулы реальных газов занимают определенный объем и взаимодействуют между собой. При больших давлениях и низких температурах становится заметным влияние собственных объемов молекул и сил взаимодействия между ними. При этих условиях уравнение Клапейрона—Менделеева и законы Бойля—Мариотта, Гей-Люссака, Шарля непригодны для описания состояния реальных газов.

В 1873 г. голландский физик И. Ван дер-Ваальс ввел в уравнение Клапейрона—Менделеева поправки на размер молекул и на действие сил притяжения между ними. И. Ван-дер-Ваальс предложил модель реального газа, в которой молекулы принимаются за твердые шарики диаметром d и занимают хоть малый, но некоторый объем. Молекулы не только отталкиваются при соударениях, но еще и притягиваются друг к другу сравнительно слабыми силами на расстояниях, сравнимых с размерами молекул.

Запишем уравнение Клапейрона—Менделеева для одного моля идеального газа (m = M): , где V_M — молярный объем газа.

Учет собственного объема молекул приводит к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V_M, a (V_M - b), где постоянная b равна приблизительно учетверенному собственному объему молекул.

Действие сил притяжения между молекулами реального газа приводит к появлению дополнительного давления на газ. При приближении некоторой молекулы к стенке сосуда все остальные молекулы оказываются по одну сторону от нее и равнодействующая сил притяжения, действующих на эту молекулу, оказывается направленной от стенки сосуда внутрь газа. Это приводит к тому, что уменьшается импульс, передаваемый молекулой стенке сосуда. В результате давление газа p на стенки сосуда уменьшается по сравнению с тем p_id, каким оно было бы в отсутствие сил притяжения: . Как показывают расчеты, это дополнительное давление обратно пропорционально квадрату объема газа, т.е.

где а — постоянная.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для одного моля газа (уравнение состояния реальных газов)

Если газ произвольной массы m занимает объем V, то его молярный объем , где количество газа . Подставив значение молярного объема, получим уравнение Ван-дер-Ваальса для произвольного числа ν молей газа:

Постоянные для каждого газа поправки a и b находят экспериментально.

Так как молекулы идеального газа не имеют объема и не взаимодействуют между собой, то идеальный газ при любых изменениях его параметров остается газом.

Совсем иначе ведут себя реальные газы. Чтобы убедиться в этом, исследуемый газ помещают в прозрачный цилиндр с подвижным поршнем (рис. 1), который помещают в термостат.

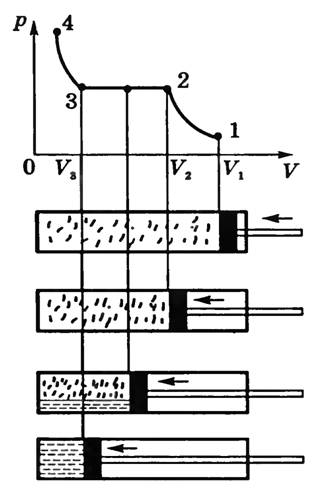
При медленном сжатии газа температура его не изменяется (процесс изотермический) и давление газа увеличивается в соответствии с законом Бойля—Мариотта. На графике эта стадия опыта изображена кривой 1-2. Но, начиная с некоторого объема, дальнейшее уменьшение объема газа уже не приводит к увеличению давления, а на стенках цилиндра появляются капельки жидкости. При этом находящиеся одновременно газ и жидкость имеют одинаковую температуру и находятся под одинаковым давлением, т.е. находятся в термодинамическом равновесии.

Газ, находящийся в термодинамическом равновесии со своей жидкостью, называется насыщенным паром.

Таким образом, участок изотермы 2-3 соответствует насыщенному пару над жидкостью (двухфазная среда). Когда весь газ превратится в жидкость, дальнейшее уменьшение объема приводит к резкому возрастанию давления (участок кривой 3-4), поскольку молекулы в жидкости упакованы достаточно плотно и ее сжимаемость мала. Вся кривая 1-2-3-4 называется изотермой реального газа.

Таким образом, изотермы реального газа заметно отличаются от изотерм идеального газа наличием у них горизонтальных участков, соответствующих области существования двухфазной системы.

Следовательно, основное отличие реальных газов от идеального состоит в том, что реальный газ может быть превращен в жидкость.

26. Изотермы Ван-дер-Ваальса.

27. Внутренняя энергия реального газа

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул, которая определяет внутреннюю энергию идеального газа и потенциальную энергию межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ

Работа, которая затрачивается на преодоление сил притяжения, действующих между молекулами газа, идет на увеличение потенциальной энергии системы.

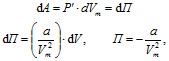
где постоянная интегрирования принята равной нулю. Знак «–» означает, что молекулярные силы, создающие внутреннее давление P′, являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа

растет с повышением температуры и увеличением объема. Если газ расширяется без теплообмена с окружающей средой, т.е. dQ = 0, и не совершает внешней работы, т.е. dA = 0, то на основании первого начала термодинамики получим, что

U1 = U2  (2).

Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется. Равенство (2) формально справедливо как для идеального, так и для реального газа, но физический смысл для обоих случаев совершенно различен.

Для идеального газа равенство (2) означает равенство температур, т.е. T1 = T2, и при адиабатическом расширении идеального газа в вакуум его температура не изменяется.

Для реального газа из равенства (2) для моля газа

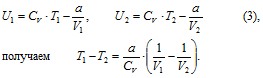
Т.к. V2 > V1, то T1 > T2, т.е. газ при адиабатическом расширении в вакуум охлаждается и наоборот, при адиабатическом сжатии в вакуум реальный газ нагревается.