5. Волновая функция и ее физический смысл.

Наличие у частицы волновых свойств приводит к тому, что в квантовой физике ей сопоставляется волновая функция (x,y,z,t).     Физический смысл волновой функции. Величина | (x,y,z,t)|²dV пропорциональна вероятности того, что частица будет обнаружена в момент времени t в объеме dV в окрестности точки (x,y,z).     Волновая функция системы невзаимодействующих частиц (r₁,r₂,...r_n,t) связана с одночастичными волновыми функциями _i(r_i,t) соотношением

(r₁,r₂,...r_n,t) = ₁(r₁,t)· ₂(r₂,t)·... _n(r_n,t).

Свободное движение частицы

    Волновая функция свободно движущейся частицы с энергией E и импульсом p имеет вид

  (r,t) = Aexp[i(kr - t)] = Aexp[i(pr - Et)/ ] .

    Константа A может быть найдена из условия нормировки волновой функции

A = (2 )^-3/2.

Т.е. в тех случаях, когда частица находится в области пространства, где действующие на нее силы равны нулю (свободное движение), энергия частицы может принимать любые значения. Энергетический спектр свободно движущейся частицы непрерывный.

6. Уравнение Шредингера для стационарных состояний

7. Частица в одномерной прямоугольной яме

8. Квантовый гармонический осциллятор

9. Молекулярно-кинетическая теория идеальных газов

10. Уравнение состояния идеального газа

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

•  — давление,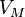

•  — молярный объём,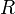

•  — универсальная газовая постоянная

•  — абсолютная температура,К.

Так как , где  — количество вещества, а , где  — масса,  — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.)

11. Основное уравнение мкт

, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул (i = 3 в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

Вывод основного уравнения мкт

Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём.

Обозначим скорость движения v_x, тогда перед столкновением со стенкой сосуда импульс частицы равен mv_x, а после — − mv_x, поэтому стенке передается импульс p = 2mv_x. Время, через которое частица сталкивается с одной и той же стенкой, равно .

Отсюда следует:

Так как давление , следовательно сила F = p * S

Подставив, получим:

Преобразовав:

Так как рассматривается кубический сосуд, то V = Sl

Отсюда: .

Соответственно, и .

Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z.

Поскольку , то . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда или .

Пусть  — среднее значение кинетической энергии всех молекул, тогда:

, откуда .

Для одного моля выражение примет вид