
- •3. Определение определителя 3-го порядка как обобщение записи определителя 2-го порядка и геометрической схемы (правила) формирования членов определителя, то есть его вычисления.
- •8,9. Миноры и алгебраические дополнения
- •18.Ранг матрицы: определение и способы его вычисления.
- •19.Определение системы линейных уравнений. Классификация систем линейных уравнений
- •20.Матричная форма записи систем линейных уравнений
- •21.Схема применения правила Крамера при решении системы линейных уравнений
- •22.Схема решения системы линейных уравнений методом Гауса
- •23.Теорема Кронекера-Капелли: с доказательством и иллюстрацией применения.
- •24.Схема исследования и решения системы линейных уравнений в общем случае.
- •31. Сложение и умножение линейных преобразований.
- •33. Вычисление собственных векторов и значений методом прямых итераций
1.
Определители второго порядка как
следствие решения системы уравнений
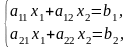 именно,
получение выражений:
именно,
получение выражений:
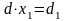 и
и
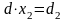 ,
где
,
где
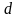 =
=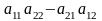 =
= ,
, =
=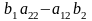 =
=
=
=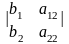 и
и
 =
= =
=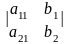 - определители 2-го порядка.
Свойства определителя
второго
порядка.
- определители 2-го порядка.
Свойства определителя
второго
порядка.
Пусть
дана квадратная таблица из четырех
чисел
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
![]() (1)
(1)
Число
![]() называется определителем второго
порядка, соответствующего таблице (1).
Этот определитель обозначается символом
называется определителем второго
порядка, соответствующего таблице (1).
Этот определитель обозначается символом
![]() ; соотвественно имеем
; соотвественно имеем
![]() (2).
(2).
Рассмотрим систему двух уравнений
![]()
![]() (3)
(3)
с
двумя неизвестными x, y. (Коэффициенты
,
,
,
и свободные члены
![]() ,
,
![]() предположим данными.) Введем обозначения
предположим данными.) Введем обозначения
![]() ,
,
![]() ,
,![]() (4)
(4)
Определитель
![]() ,
составленный из коэффициентов при
неизвестных системы (3), называется
определителем этой системы. Определитель
,
составленный из коэффициентов при
неизвестных системы (3), называется
определителем этой системы. Определитель
![]() получается путем замены элементов
первого столбца определителя
свобдными членами системы (3); определитель
получается путем замены элементов
первого столбца определителя
свобдными членами системы (3); определитель
![]() при помощи замены свободными членами
системы (3) элементов его второго столбца.
при помощи замены свободными членами
системы (3) элементов его второго столбца.
Если
![]() ,
то система (3) имеет единственное решение;
оно определяется формулами
,
то система (3) имеет единственное решение;
оно определяется формулами
![]() ,
,![]() .
.
Если и при этом хотя бы один из определителей , отличен от нуля, то система (3) совсем не имеет решений (как говорят, уравнения этой системы несовместны).
Если
же
![]() , но также
, но также
![]() ,
то система (3) имеет бесконечно много
решений (в этом случае одно из уравнений
системы есть следствие другого).
,
то система (3) имеет бесконечно много
решений (в этом случае одно из уравнений
системы есть следствие другого).
2.
Геометрический смысл решения системы
двух уравнений с двумя неизвестными.
Что значит каждая из ситуаций: а)
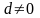 ;
б)
=0
и
=
=0;
в)
=0
и хотя бы одно из чисел
,
;
б)
=0
и
=
=0;
в)
=0
и хотя бы одно из чисел
,
 0.
0.
Пусть
на плоскости задана аффинная система
координат
![]() . Как показано ниже, множество точек
. Как показано ниже, множество точек
![]() ,
координаты которых удовлетворяют
линейному уравнению с двумя неизвестными
,
координаты которых удовлетворяют
линейному уравнению с двумя неизвестными
![]() ,
или
,
или
![]() ,
представляет собой прямую. Поэтому
множество решений системы уравнений
является пересечением прямых
,
представляет собой прямую. Поэтому
множество решений системы уравнений
является пересечением прямых
![]() .
.

3. Определение определителя 3-го порядка как обобщение записи определителя 2-го порядка и геометрической схемы (правила) формирования членов определителя, то есть его вычисления.
Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
![]() .
.
Данная формула получила название правила треугольников или правило Сарруса.
При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:

4. . Свойства определителя 3-го порядка, вытекающие из принятого правила его вычисления. Вычисление определителя 3-го порядка разложением по столбцу (строке).
а)Свойство 1. Если все элементы какой-либо строки (столбца) определителя 3-го порядка равны нулю, то и определитель равен нулю.
Свойство 2. Определитель 3-го порядка не изменится, если его строки заменить столбцами с теми же номерами.
Свойство 3. Если поменять местами две строки (столбца) определителя 3-го порядка, то обсолютная величина определителя не изменится, а знак изменится на противоположный.
Следствие. Определитель 3-го порядка, в котором каких-либо две строки (столбца) совпадают, равен нулю.
Свойство 4. Если все элементы какой-либо строки (столбца) определителя 3-го порядка умножить на какое-либо число, то и определитель умножится на это число.
Следствие 1. Если все элементы какой-либо строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя.
Следствие 2. Если все элементы какой-либо строки (столбца) определителя 3-го порядка пропорциональны соответствующим элементам другой строки (столбца) этого определителя, то определитель равен нулю.
Свойство 5. Если каждый элемент какой-либо строки (столбца) определителя 3-го порядка представляет собой сумму двух слагаемых, то и определитель можно представить в виде суммы двух слагаемых, например:
a1b1c1 + d1 a1b1c1 a3b3c3
a2b2c2 + d2 = a2b2с2 + a2b2d2
a3b3c3 + d3 a3b3c3 a3b3d3
б)Если D = |A| - определитель порядка n, то минором Mij элемента аij называют определитель порядка n-1, получающийся из D вычеркиванием i-й строки и j-го столбца. Под алгебраическим дополнением Aij элемента аij понимают минор Mij, домноженный на (-1)i+j, т.е. Aij = (-1)i+jMij
5.
Система трех линейных уравнений с тремя неизвестными имеет вид
![]()
![]()
![]()
![]() (7)
(7)
Определитель
![]()
![]()
![]() (8)
(8)
составленный из коэффициентов при неизвестных, называется определителем системы.
1. Если определитель системы , то система (7) имеет решение, и притом единственное. Это решение находится по формулам
![]()

![]()

![]()
 (9)
(9)
Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.
Определители, стоящие в числителях дробей (9), будем обозначать соответственно через Dx, Dy, Dz.
2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей Dx, Dy и Dz не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.
3. Если D = 0 и все определители, стоящие в числителях дробей (9), - Dx, Dy, Dz - равны нулю, т. е. если
D = Dx = Dy = Dz = 0,
но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.
4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей Dx, Dy, Dz не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.
5. Если в определителях D, Dx, Dy, Dz все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.
7.Пусть дана квадратная таблица, состоящая из чисел, расположенных в n горизонтальных и в nвертикальных рядах. С помощью этих чисел по определённым правилам вычисляют некоторое число, которое называют определителем n-го порядка и обозначают следующим образом:
 (1)
(1)
Горизонтальные
ряды в определителе (1) называют строками,
вертикальные – столбцами,
числа ![]() -элементами определителя
(первый индекс означает номер строки,
второй – номер столбца, на пересечении
которых стоит элемент; i = 1, 2, ..., n;
j = 1, 2, ..., n). Порядок определителя
– это число его строк и столбцов.
-элементами определителя
(первый индекс означает номер строки,
второй – номер столбца, на пересечении
которых стоит элемент; i = 1, 2, ..., n;
j = 1, 2, ..., n). Порядок определителя
– это число его строк и столбцов.
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
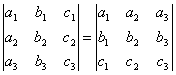 .
.
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,
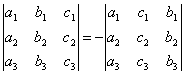 .
.
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
 .
.
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,

СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
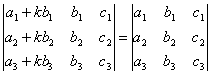 .
.
Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.
СВОЙСТВО 9. Определитель
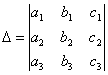
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
