44. Формула Рэлея-Джинса

Рэлей и Джинс в 1900–1905 г. сделали попытку определить функцию спектрального распределения энергетической светимости, исходя из теоремы о равномерном распределении энергии по степеням свободы.

Представим себе вакуумированую полость, стенки которой поддерживаются при постоянной температуре Т. В равновесном состоянии энергия излучения будет распределена в объеме полости с определенной плотностью, которая зави­сит только от температуры и не зависит от свойств сте­нок полости. Ученые исходили из того, что равновесное излучение в полости представляет собой систему стоячих волн. На каждое электромагнитное колебание приходится в среднем энергия, равная двум половинкам kT: ½kT – на электрическую, ½kT – на магнитную энергию волны (по классическим представлениям на каждую колебательную степень свободы приходится в среднем энергия, равная kT). Для функции спектрального распределения энергии равновесного излучения в полости, приходящуюся на диапазон длин волн dλ, Рэлей и Джинс получили формулу:

.

Или в зависимости от частоты света:

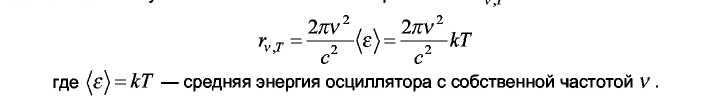
В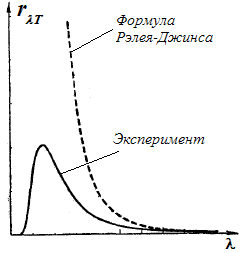 ыражение получило название формулы Рэлея-Джинса. Эта формула удовлетворяет экспериментальным данным лишь при больших длинах волн (см. рис.). Интегрирование выражения по всем длинам волн в пределах от 0 до ∞ дает бесконечно большое значение. Отсюда следует, что по теории Рэлея-Джинса тепловое равновесие между излучением и веществом невозможно. Этот вывод, названный ультрафиолетовой катастрофой, противоречит опыту. Причина ультрафиолетовой катастрофы заключается в том, что в теории Рэлея-Джинса излучение в полости имеет бесконечное число степеней свободы, а вещество – конечное. Поэтому, если бы было справедливо равномерное распределение энергии по степеням свободы, то при тепловом равновесии вся энергия должна была бы сосредоточиться в излучении.

45. Формула Планка

Формула Планка. Правильная формула для спектральной плотности энергетической светимости равновесного излучения, подтвержденная всеми экспериментальными исследованиями, была найдена Планком сначала полуэмпирическим путем. Спустя короткое время, Планк нашел теоретический вывод этой формулы, изложенный им 14 декабря 1900 г. на заседании Немецкого физического Общества. Этот день считается днем рождения квантовой физики.

Гипотеза Планка состоит в том, что излучение и поглощение света веществом происходит не непрерывно, а дискретными порциями, называемыми квантами, величина которых пропорциональна частоте излучения. Энергия кванта: ,

где – постоянная Планка.

Формула Планка может быть получена тем же методом, что и формула Рэлея-Джинса. Согласно Планку, энергия гармонического осциллятора может принимать не произвольные, а только избранные значения, образующие дискретный ряд: Под осциллятором понимается не только частица, совершающая гармонические колебания, но, например, и стоячая волна определенной частоты в полости. Если осциллятор находится в полости, стенки которой поддер­живаются при постоянной температуре, то наряду с излучением будут происходить и акты поглощения. Со временем установится вполне определенное состояние детального равновесия, в котором число актов излучения в среднем равно числу обратных актов поглощения. Планк доказал, что средняя энергия осциллятора может быть определена как

.

Подставив выражение в формулу Рэлея-Джинса вместо kT, получим, что универсальная функция Кирхгофа принимает вид

.

И называется формула Планка.

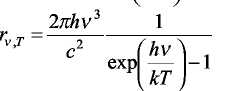
В области больших длин волн , тогда , и формула переходит в формулу Рэлея-Джинса.