3 Закон наименьшего сопротивления

При обработке металлов давлением иногда необходимо опре­делять соотношение между перемещениями металла в разных направлениях. В некоторых случаях эти соотношения легко оп­ределить на основании условия постоянства объема. Так, при осадке цилиндрического образца, волочении круглой проволоки минимальная деформация равна половине максимальной.

При осадке параллелепипеда с трением на контактной поверх­ности последнее создает сопротивление течению металла в горизонтальной плоскости, разное по величине в направлении длин­ной и короткой сторон прямоугольника.

Качественно направление течения металла в этом случае оп­ределяют на основании закона наименьшего сопротивления, который формулируется так: «В случае возможности перемещения точек деформируе­мого тела в различных направлениях каждая точка деформируемого тела перемещается в направлении наименьшего сопротивления».

Установлен также принцип наименьшего периметра: любая форма цилиндрического или призматического тела при осадке с наличием контактного трения будет стремиться к форме с наименьшим периметром, т.е. к кругу.

На основании этого можно предсказать конечную форму деформируемого тела: периметры поперечного сечения осаживаемых образцов квадратного сечения и параллелепипеда будут стремиться к кругу

Схема течения металла при осадке образца прямоугольного сечения..

Схема течения металла при осадке прямоугольного образца

.

4. Закон подобия при омд

Подобными условиями деформации называют такие, которые должны удовлетворять условиям геометрического, механического и физического подобия.

Геометрическое подобие.

В. Л. Кирпичев в 1874 г. сформулировал закон подобия для упругой деформации металлов. Согласно этому закону, работы деформации геометрически подобных тел, изготовленных из одного и того же материала, пропорциональны объемам, а уси­лия — сходственным площадям; при этом удельные усилия равны.

Ф. Кик в 1879 г. предложил распространить этот закон и на пластическую деформацию.

Согласно за­кону подобия деформируемые тела должны быть геометрически подобны и физически одинаковы.

Геометрическое подобие будет соблюдено, если отношения сходственных линейных размеров (длина l, ширина b, высота h) модели (с индексом «м») и натуры (с индексом «н») будут оди­наковы, т. е.

( 1)

где п — масштаб моделирования.

Отношения сходственных площадей будут пропорциональны квадрату масштаба моделирования, а отношения объемов — кубу.

Для соблюдения геометрического подобия в процессе деформации необходимо, чтобы степени деформации модели и натуры ■были равны:

(2)

Технологический инструмент для деформирования модели и натуры должны быть также геометрически подобны и отношение их линейных размеров должно быть равно масштабу моделирования.

Физическое подобие. Для осуществления физического подобия необходимо, чтобы

физические свойства модели и натуры (химический состав, фазовое состояние, микро- и макроструктура) в исходном со­стоянии и в каждый момент деформации были одинаковые. Кроме этого, должны быть равны и коэффициенты трения на контактных поверхностях.

При пластической деформации обеспечить одинаковые физи­ческие свойства модели и натуры (особенно в интервале температур фазовых превращений) невозможно. Объясняется это тем, что отношение скоростей и продолжительности деформирования, а следовательно, и скоростей деформации модели и натуры дол­жно быть различным для обеспечения одинаковой температуры, одинаковых условий трения и условий протекания процессов упрочнения и разупрочнения.

Для обеспечения одинаковой температуры модели и натуры в процессе деформации при одинаковой исходной необходимо скорость деформирования модели увеличить в п раз, так как мо­дель охлаждается быстрее вследствие большего в п раз отноше­ния поверхности к объему. Следовательно, для соблюдения теп­лового подобия (равенства температур) необходимо, чтобы

., (3)

Тогда отношение скоростей деформации модели и натуры будет равно квадрату масштаба моделирования:

(4)

Продолжительность деформирования модели должна быть в п² раз меньше продолжительности деформирования натуры:

(5)

Для соблюдения одинаковых условий трения, помимо одинако­вых материалов инструмента, качества обработки его поверхно­сти, смазки и температуры, необходимо обеспечить одинаковую скорость скольжения металла по инструменту. Последнее воз­можно только при одинаковых скоростях деформирования моде­ли и натуры:

(6)

Скорость деформации модели должна быть в п раз больше скорости деформации натуры:

(7)

Продолжительность деформации модели

(8)

Для соблюдения одинаковых условий протекания процессов упрочнения и разупрочнения при одинаковых степенях деформа­ции, необходима одинаковая скорость деформации:

(9)

Тогда скорость деформирования модели должна быть в п раз меньше скорости деформирования натуры:

(10)

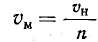
Продолжительность деформирования натуры и модели должна быть одинакова:

(11)