24. Сходимость случ величин по вер-м

Если треб узнать число а с погр σ, то найдется такое число n, что для номеров > чем n, погрешн от замены А на а_n будет < ε. Опред предел послед случ велич: ξ₁, ξ_2… ξ_n сходятся по вероятн к числу а, если для любого ε вероят того, что ξ_n – а <ε 1.

P(|ξ –a| < ε) = γ – погрешн от замены ξ числом а, сама величина – это надежность этой замены. ξ_n≈а Какая ни была бы точность, но надежность стремится к 1.

25.Зак больш чисел для сх Бернулли

С х Бернулли – это послед незав испытаний в каждом из кот соб А осущ пост с вероятностью

А -успех Р(А)=р, А-неудача Р(А)=q

Пусть i-сл вел= в i-м испытании

Такая величин

Явл индикатор успеха. _n=1+2+…+n –число успеха в n-испыт М_n/n=М((1+…+n)/n)=p

D_n/n=pq. Применим ннер-во Чебышева:

Следствие1:

Средн арифм сходится по вер-ти к P(вер-ть успеха в А). Kn(A)=m_n(A)\nP(A) Kn(A)-астота событ А m_n(A)\n-вер-ть этого соб

Ч астота стремится к некотор числу, котор и будет вер-м. Следствие2:

Это ннер-во дает

оценку вероят отклон частоты от вер Р.

26. Центр пред теор и лок для форм для сх Берн Пусть ξ₁, ξ ₂… ξ _n-независ. Mξ_i=a; Dξi=σ²

Центральная предельная теорема утвержд, что

Вер-ть _n попадет в промеж (_n)

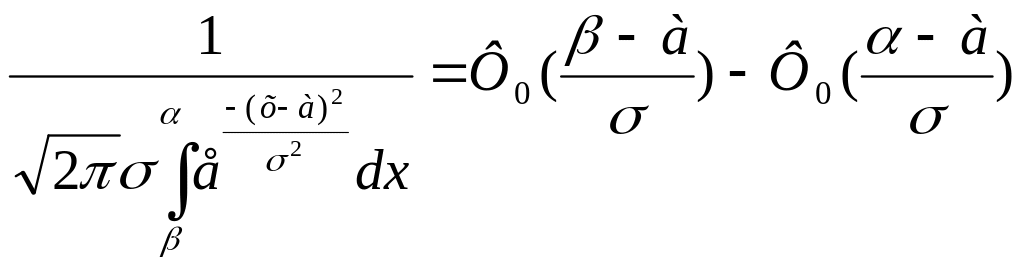стремиться к:

Вер-ть того, что норм распред СВ попадает в промеж (α;β)

Следствие:Если в кач-ве

ξ₁, ξ ₂… ξ _n брать индикаторы успеха в схеме Бернулли, то вер-ть того что Р((_n/n))→

Если домножить на n то:

интегральная теор Лапласа т.е центр пред теор. Это обобщ инт теор Лапласа

27. Корреля́ция-статистическ взаимосв двух или нескольких СВ. Если сл вел ,-могут быть завис и независ Р(х;у)= Р(х)* Р(у)

Если зависим, как характериз меру зав-ти?

Пусть -цена на тов, - Vпродаж. Мера зависим

1,1=М((-М)(-М))-если , независимы

Коэфиц корреляции: К=1,1/σ_ σ_ Свойства: 1) если ξ, η-нез. =>k=0

2) |k| ≤1; 3) если ξ и η линейнозавис. ξ=аη + b, то |k| ≤1 и наоборот. Тогда коэф. кореляц. – мера линейной завис СВ. Если k=0, то СВ некор-ая; k=1 то СВ- корялиров. Док-во:

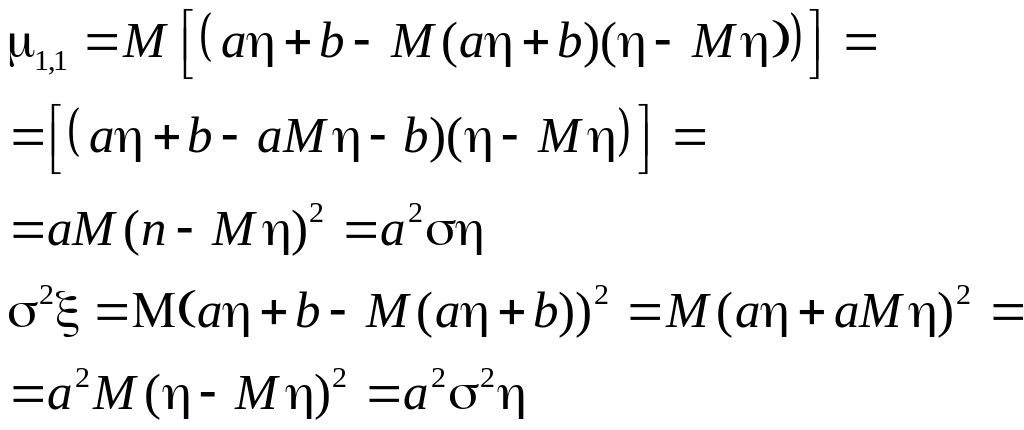
3 6. Критерий согл хи-квадрат. Дан крит позвол кол-но оцен степень соглас выбороч данных провер гипотезы. Для пр-ки г-зы разб обл знач на s интер-л; подсчит вер-ти попад наблюд X в интер-л с помощью ф-лы P(α≤X≤β)==Ф₀(β)-Ф₀(α). Пров-ем г-зу с пом кр-ия χ²: n_i-империч частоты,

n_i’-теоретич частот (n_i’=np_i).

При n→∞ статистика имеет χ²-распред с k=s-1-r. s- число интер-ов, к-число пар-ов предлаг распр-ия. Если предл распр-ие нормально – оцен 2 критерия (а и σ). Поэтому r=2 и ч-ло степ свобод k=s-3. Пр-ло примен критерия χ²:1)по ф-ле (*) вычис χ²_набл-выбороч знач ст-ки кр-ия.2)Выбрав ур-нь знач-ти α кр-ия, по табл распр χ² наход критич точку (квантиль) χ²_α,k. 3) χ²_набл≤ χ²_α,k – г-за приним; χ²_набл> χ²_α,k- г-за отверг. Необход усл-ие: n_i≥5. Если чило наблюд мен, то инт-лы объедин.

3 7. Лин модель. Нахожд её коэф по методу наим кв-тов. Пример: Пусть некот фирмы прод пр-кт Y и у них нек рес-сы X, x_1…x_n. Чего зав V продаж?

Если влож ст-ко денег

В x₁ – на ст-ко увел V

прод

…………………..

С чит, что это случ вел-ны и они завис.

- мат модель

(2)

………………………

С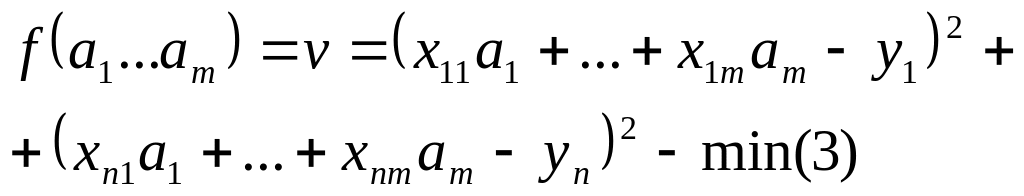 чит, что n>m. “Эта с-ма обыч несовм, т е не имеет реш.

Найд мин приров производ к нулю:

Метод нахожд реш с-мы (2)- «метод наим квадратов». С-ма (4) будет определ с-мой.

38. случ процессы и их хар-ки. Случ процессом ( или ф-ей) наз ф-ия котор кажд эл-ту мн-ва t ставит в соответствие случ вел-ну. Таким образом случ процесс записX(t), ξ(t).

t обыч предст как время. F(x,t)=P(X(t)<x) – ф-ия распр-ия кажд сечения X(t)

Хар-ки: Мат ожидание MX(t)→m(t) ф-ия не случ, завис от t. Зав-сть случ вел-н между различ вел-ми: μ(t1,t2)=M(X(t1))-m(t1))/X(t2)-m(t2)) – корреляц момент.Чем дальше t1 от t2 тем менее зависимы случ вел-ны, тем ближе к 0 корреляц момент.