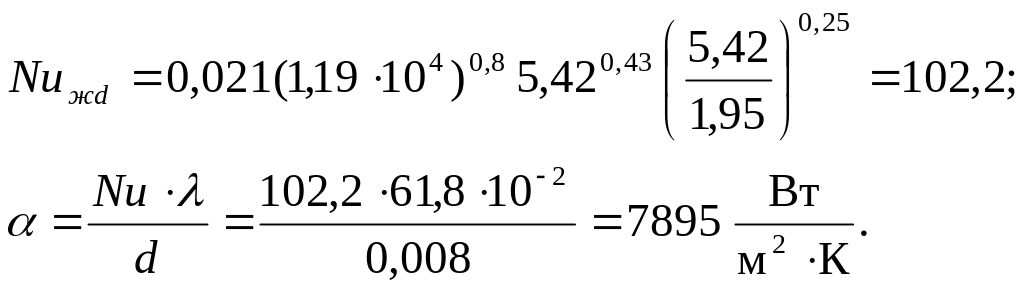Решение

При средней температуре воды в трубке =30^оС из табл. 2 приложения имеем:

при температуре стенки t_с=90^оС Pr_c=1,95.

Определяем число Рейнольдса

Режим течения турбулентный. По уравнению (7.28) рассчитываем средний коэффициент теплоотдачи от стенки трубки к воде. Так как /d=5/0,008=625>50, то =1,

Тепловой поток

8. Теплоотдача при фазовых превращениях

8.1. Теплоотдача при кипении

Кипение – это процесс образования пара при подводе тепла к кипящей жидкости.

Тепловой поток, подводимый к кипящей жидкости, расходуется на процесс парообразования

(8.1)

где F, м² – площадь поверхности нагрева;

Т_с – температура поверхности;

T_s - температура насыщения;

G, кг/с – количество образовавшегося пара за 1с (расход пара);

r –Дж/кг – теплота парообразования.

Уравнение (8.1) является уравнением теплового баланса процесса кипения.

Для возникновения процесса кипения необходимы два условия:

1. Наличие перегрева жидкости относительно температуры насыщения (t_s), рис. 8.1.

Для воды при атмосферном давлении перегрев ΔТ=T_ж-T_s=0,20,4С, максимальный перегрев ΔТ=T_с-T_s может составлять 3150^оС и выше.

2 . Наличие центров парообразования, которыми могут служить микрошероховатости поверхности нагрева, адсорбированные поверхностью пузырьки газа, твердые частицы.

Кипение может происходить во всем объеме жидкости или на твердой поверхности нагрева. В промышленных устройствах кипение, как правило, происходит на поверхности нагрева и может осуществляться в условиях естественной конвекции (кипение в большом объеме) или принудительной циркуляции.

Кипение может быть пузырьковым или пленочным.

При пузырьковом кипении пар образуется в виде пузырьков, периодически зарождающихся около центров парообразования. Зародившийся паровой пузырек с минимальным (критическим) радиусом (r_к) растет, вследствие подвода теплоты, до отрывного диаметра (d₀), затем отрывается от поверхности нагрева и всплывает. Около освободившегося центра парообразования вновь зарождается паровой пузырек. Этот процесс периодически повторяется с определенной частотой – частотой отрыва парового пузырька (f). Величина w=d₀ f характеризует среднюю скорость роста паровых пузырей.

При пленочном кипении, которое характеризуется большими перегревами (Т_с-Т_s), у поверхности нагрева образуется паровая пленка, отделяющая жидкость от поверхности. Теплопроводность пара значительно меньше, чем жидкости, поэтому интенсивность теплообмена при пленочном кипении в десятки раз ниже, чем при пузырьковом.

Интенсивность теплоотдачи при пузырьковом кипении зависит от микрохарактеристик и режимных параметров процесса кипения.

К микрохарактеристикам относятся:

• минимальный (критический) радиус парового пузыря (r_к);

• отрывной диаметр пузыря (d₀);

• частота отрыва (f) и скорость роста (w) пузырей.

К режимным параметрам относятся:

• давление кипящей жидкости (р);

• перегрев жидкости (ΔТ=T_с-T_s);

• тепловой поток, подводимый к 1 м² поверхности нагрева (q);

• скорость движения кипящей жидкости (w).

Теоретически и экспериментально установлено, что с увеличением р, ΔТ, q улучшаются все макрохарактеристики процесса кипения, увеличивается теплоотдача.

Теплоотдача при кипении зависит от свойств кипящей жидкости растет:

• с увеличением коэффициента теплопроводности ();

• с уменьшением коэффициента поверхностного натяжения ();

• с уменьшением вязкости жидкости (v).

Влияние на теплообмен при кипении оказывают состояние поверхности нагрева, ее материал, смачиваемость, количество адсорбированных газов и свойства греющей стенки. Теплоотдача растет с увеличением шероховатости поверхности, теплопроводности и толщины греющей стенки. Все эти факторы влияют на число центров парообразования.

И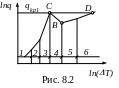 нтенсивность теплоотдачи при пузырьковом кипении практически не зависит от формы и размеров теплоотдающей поверхности.

На рис. 8.2 приведена зависимость теплового потока от температурного напора ln q=f (ln ΔТ) при кипении жидкости - кривая кипения.

При подводе тепла к поверхности нагрева в условиях естественной конвекции повышается температура поверхности (Т_с), жидкость воспринимает теплоту, нагревается и кипит.

Можно выделить следующие участки кривой кипения, рис. 8.2.:

1. - конвективный теплообмен;

2. - конвективный теплообмен со слабым кипением жидкости;

3. – развитое пузырьковое кипение;

4. – переходная область от пузырькового кипения к пленочному;

5. – пленочное кипение;

6. – пленочное кипение со значительным лучистым теплообменом через паровую пленку.

При максимальном значении теплового потока ( ) наступает кризис кипения, который заключается в изменении режима кипения; называют первой критической плотностью теплового потока.

При кипении жидкостей на горизонтальной плоской поверхности в условиях естественной конвекции первая критическая плотность теплового потока рассчитывается по формуле

(8.2)

где r, Дж/кг – теплота парообразования; _п, _ж – плотность паровой и жидкой фаз при температуре насыщения t_s; , Н/м – коэффициент поверхностного натяжения жидкости; g =9,8 м/с².

Постепенный переход пузырькового режима в пленочный, осуществляемый на участке СВ на практике реализуется при омывании другой стороны теплопередающей поверхности горячим конденсирующимся паром. В этом случае температура поверхности (Т_с), а следовательно, перегрев жидкости (Т) определяется давлением конденсирующегося пара и от процесса кипения не зависит.

При электрическом обогреве поверхности или радиационном (в паровых котлах) переход пузырькового кипения в пленочное произойдет скачкообразно (линия СD, рис. 8.2) и может сопровождаться сильным перегревом и разрушением поверхности нагрева. Поэтому в промышленных теплообменниках с кипением жидкостей не допускают q= , обеспечивают q< .

Расчет теплоотдачи при пузырьковом кипении

Сложные явления, наблюдающиеся при пузырьковом кипении, не дают возможности составить физически правильную модель процесса и дать ее полное математическое описание.

Для пузырькового кипения жидкости в условиях естественной конвекции (в большом объеме) предложен ряд формул для определения коэффициентов теплоотдачи. Например, формула, предложенная Д.А.Лабунцовым, которая с максимальным отклонением  35 % отражает экспериментальные данные многих исследований по кипению различных жидкостей в самых разнообразных условиях, имеет вид

(8.3)

где , _ж, v_ж, _ж – коэффициент поверхностного натяжения, теплопроводность, вязкость, плотность жидкости при t_s; _п – плотность пара при t_s; q, Вт/м² – плотность теплового потока, подводимого к поверхности нагрева.

Формула (8.3) применительно к воде имеет вид

(8.4)

и применима в диапазоне давлений от 1 до 200 бар. Давление р в формулу (8.4) должно подставляться в барах.

Подстановка q=(t_c-t_s) в (8.4) дает расчетную формулу для коэффициента теплоотдачи в виде

(8.5)

В практических расчетах пользуются эмпирическими зависимостями коэффициента теплоотдачи от режимных параметров. Например, для воды в интервале давлений р=140 бар можно воспользоваться формулами

=3,0 q0,7 p0,15,	(8.6)
=38,7 t 2,33 p0,5,	(8.7)

где р, бар; q, Вт/м²; , Вт/м²К.

При вынужденном течении кипящей жидкости в трубах на интенсивность теплообмена влияет соотношение процесса кипения и вынужденной конвекции. Если скорость вынужденного течения жидкости мала, то интенсивность теплоотдачи определяется, главным образом, наличием действующих центров парообразования, т.е. процессом кипения. При больших скоростях вынужденное течение подавляет влияние кипения. Значение коэффициента теплоотдачи  при вынужденном течении кипящей жидкости в трубах рекомендуется определять в зависимости от соотношения между коэффициентом теплоотдачи _q, рассчитанным по одной из формул (8.3) – (8.7), и коэффициентом теплоотдачи _w, рассчитанным по формулам конвективного теплообмена при вынужденном течении однофазной жидкости в трубах (7.26) – (7.28).

Если _q/_w0,5, то =_w;

если _q/_w2, то =_q;

при 0,5<_q/_w<2 следует воспользоваться интерполяционной формулой

(8.8)