1)Высказывания и операции над ними. Под высказыванием понимают грамматически правильное повествовательное предложение, про которое можно сказать, что оно либо истинно, либо ложно

1) отрицание: А

2) дизъюнкция: А  В

3) конъюнкция: А  В

4) импликация: А → В

5) эквивалентность: В ~ А

2)Формулы А.В и их виды

1.
2.	Законы
3.	де Моргана
4.
5.

Эти фомулы могут быть доказаны сравнением соответствующих таблиц истинности.

Из двух высказываний А и В можно составить четыре импликации, которые носят название

A B прямая теорема B A обратная теорема противоположная теорема теорема противоположная к обратной

Из основных формул алгебры высказываний следует, что

( A B ) ( ) ( B A ) ( )

Следует отметить, что из истинности прямой теоремы еще не следует истинность обратной к ней теоремы, как это видно из примера 1.1.1.

Доказать истинность теоремы ( A B ) можно, доказав истинность теоремы ( ) , так как эти теоремы эквивалентны. На этом основано доказательство от противного теоремы ( A B ) , а именно, имея истинность , предполагая истинность , и доказав, что из следует , мы получаем противоречие ( A и одновременно истинны ), что не может быть, значит - ложно, тогда В - истинно и, значит, импликация A B - истинна.

3) Правила получения тавтологий. Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных. Вот несколько широко известных примеров тождественно истинных формул логики высказываний:

Законы де Моргана:

1) ;

2) ;

Закон контрапозиции:

;

Законы поглощения:

1) ;

2) ;

Законы дистрибутивности:

1) ;

2) .

4)Логическое следствие.

Доказательство теорем сводится к доказательству того, что некоторая формула (гипотеза теоремы) является логическим следствием множества формул (допущений). Т.е. сама теорема может быть сформулирована следующим образом: "если истинны, то истинна и ". Такой метод доказательства теорем называется методом резолюций.

Для доказательства того, что формула G является логическим следствием множества формул , метод резолюций применяется следующим образом. Сначала составляется множество формул . Затем каждая из этих формул приводится к КНФ (конъюнкция дизъюнктов) и в полученных формулах зачеркиваются знаки конъюнкции. Получается множество дизъюнктов S. И, наконец, ищется вывод пустого дизъюнкта из S. Если пустой дизъюнкт выводим из S, то формула G является логическим следствием формул . Если из S нельзя вывести #, то G не является логическим следствием формул .

5) Равносильность.Определение. Пусть А и В – две формулы, зависящие от одного и того же списка переменных. Будем называть их равносильными, если для любого набора значений переменных  они принимают одинаковые значения.

Рассмотрим основные равносильности логики высказываний.

Пусть А, В, С – произвольные формулы. Тогда справедливы следующие свойства логических операций

1. Идемпотентность
А Щ А = А	А Ъ А = А
2. Коммутативность
А Щ В = В Щ А	А Ъ В = В Ъ А
3. Ассоциативность
А Щ (В Щ С) = (А Щ В) Щ С	А Ъ (В Ъ С) = (А Ъ В) Ъ С
4. Правила поглощения
А Щ (А Ъ В) = А	А Ъ (А Щ В) = А
5. Дистрибутивность
А Щ (В Ъ С) = (А Щ В) Ъ (А Щ С)	А Ъ (В Щ С) = (А Ъ В) Щ (А Ъ С)
6. Правила де Моргана
7. Свойства констант
А Щ 1 = А А Щ 0 = 0	А Ъ 0 = А А Ъ 1 = 1
8. Закон исключения третьего и закон противоречия
9. Снятие двойного отрицания
10. Формулы расщепления (склеивания)
11. Связь  дизъюнкции, конъюнкции, отрицания и импликации
12. Выражение эквивалентности

6) Бинарное отношение на множестве называется отношением эквивалентности, если оно обладает следующими свойствами:

• Рефлексивность: .

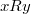• Симметричность: если , то .

• Транзитивность: если и , то .

Отношение эквивалентности обозначают символом . Запись вида читают как " эквивалентно "

• Отношение равенства( ) является тривиальным примером отношения эквивалентности на любом множестве.

• Отношение равенства по модулю : на множестве целых чисел.

• Отношение параллельности прямых на плоскости.

• Отношение подобия фигур на плоскости.

• Отношение равносильности на множестве уравнений.

• Отношение связности вершин в графе.

• Отношение быть одного роста на множестве людей.

Следующие отношения не являются отношениями эквивалентности:

• Отношения порядка, так как они не являются симметричными.

• Отношение быть знакомым на множестве людей, так как оно не транзитивное.

Определение:
Система непустых подмножеств множества называется разбиением данного множества, если: при . Множества называются классами данного разбиения.

 

 7)   Основные равносильности      Закон двойного отрицания

     Идемпотентность

     Коммутативность

     Ассоциативность

     Дистрибутивность

    Законы де Моргана

     Формулы с константами

8)Алгоритм построения днф

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Алгоритм построения кнф

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

9)Если в какой-то простой конъюнкции недостает переменной, например, Z, вставляем в нее выражение :,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:

-Y-ZV-X-Y-Z

Таким образом, из ДНФ получили СДНФ.

Если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение : (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):

-YV-Z)

Таким образом, из КНФ получена СКНФ.

Булевы функции

1)

Унарные функции

При n = 1 число булевых функций равно 2²¹ = 2² = 4. Определение этих функций содержится в следующей таблице.

Таблица значений булевых функций от одной переменной:

x	0	x̅	x	1
0	0	1	0	1
1	0	0	1	1
0					тождественный ноль, тождественная ложь, тождественное "НЕТ"
x̅, ¬x, x'					отрицание, логическое "НЕТ", "НЕ", "НИ", "NOT"(англ.), "NO"(англ.)
x					тождественная функция, логическое "ДА", "YES"(англ.)
1					тождественная единица, тождественная истина, тождественное "ДА", тавтология

2) Бинарные функции

При n = 2 число булевых функций равно 2^2² = 2⁴ = 16.

x	y	0	x↓y	x←y	x	x→y	y		x⊕y	x|y	x & y	x ≡ y	y	x→y	x	x←y	x ∨ y	1
0	0	0	1	0	1	0	1		0	1	0	1	0	1	0	1	0	1
0	1	0	0	1	1	0	0		1	1	0	0	1	1	0	0	1	1
1	0	0	0	0	0	1	1		1	1	0	0	0	0	1	1	1	1
1	1	0	0	0	0	0	0		0	0	1	1	1	1	1	1	1	1
0								тождественный ноль, тождественная ложь, тождественное "НЕТ"
x ↓ y, x ИЛИ-НЕ y, ИЛИ-НЕ(x,y), x NOR y, NOR(x,y)								НЕ- 2ИЛИ, 2ИЛИ-НЕ, антидизъюнкция, функция Да́ггера, функция Ве́бба, стрелка Пи́рса
x < y, x ← y, x LT y, LT(x,y)								меньше, инверсия обратной импликации
x, НЕ1(x,y), NOT1(x,y), x', ¬x								отрицание (негация, инверсия) первого операнда
x > y, x → y, x GT y, GT(x,y)								больше, инверсия прямой импликации
y, НЕ2(x,y), NOT2(x,y), y', ¬y								отрицание (негация, инверсия) второго операнда
x ⊕ y, x +2 y, x ≠ y, x >< y, x <> y, x XOR y, XOR(x,y)								сложение по модулю 2, не равно, измена, исключающее «или»
x | y, x NAND y, NAND(x,y), x И-НЕ y, И-НЕ(x,y)								НЕ-2И, 2И-НЕ, антиконъюнкция, штрих Ше́ффера
x & y, x · y, xy, x ∧ y, x AND y, AND(x,y), x И y, И(x,y), min(x,y)								2И, конъюнкция
x ≡ y, x = y, x EQV y, EQV(x,y), x ~ y, x ↔ y								равенство, эквивалентность
y, ДА2(x,y), YES2(x,y)								второй операнд
x → y, x ≤ y, x ⊃ y, x LE y, LE(x,y)								меньше или равно, прямая (материальная) импликация (от первого аргумента ко второму)
x, ДА1(x,y), YES1(x,y)								первый операнд
x ← y, x ≥ y, x ⊂ y, x GE y, GE(x,y)								больше или равно, обратная импликация (от второго аргумента к первому)
x ∨ y, x + y, x ИЛИ y, ИЛИ(x,y), x OR y, OR(x,y), max(x,y)								2ИЛИ, дизъюнкция тождественная единица, тождественная истина, тождественное "ДА", тавтология
5) Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой другой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством P2. Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций: Функции, сохраняющие константу T0 и T1; Самодвойственные функции S; Монотонные функции M; Линейные функции L. Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с P2, целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию. Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.

           Определение. Алгеброй Жегалкина называется алгебра над множеством логических функций и переменных, сигнатура которой содержит две бинарные операции   &   и    , и две нульарные операции – константы 0 и 1.

            В алгебре Жегалкина выполняются следующие соотношения:

1.   x  y = y  x;

2.   x ( y  z )  =  x y  x z;

3.   x  x = 0; 

                                                                                                          (1.4)

4.   x    = 1; 

5.   x  0 = x.

            Эти соотношения легко проверить табличным способом. Кроме перечисленных соотношений в алгебре Жегалкина выполняются соотношения булевой алгебры относительно конъюнкции и констант

.

            Найдем выражения для основных элементарных функций алгебры логики в алгебре Жегалкина.

1.         =  x  1. 

Это соотношение проверяется непосредственной подстановкой 0 и 1 в обе части равенства.

      x  y  =  x y  x  y.

Доказательство:                       x  y  =   =      1  =  ( x  1 )( y  1 )  1 =   

                                                       =  x y  x  y 1  1  =  x y  x  y.

3.      x  ’  y  =  x y  x  1. 

Доказательство:     Используем выражение для импликсации в (1.3). Тогда: 

     x ’ y  =    y  =    y      y   =  ( x 1 ) y  ( x  1 ) y  = 

                                   =  x y  y  x  1  y  =  x y  x  1. 

4.      x  /  y  =  x y  1.

Доказательство: Используем выражение для     x / y    в (1.3). Тогда:

                                                        x / y =  = xy  1. 

5.      x “ y  =  x y  x  y  1.

Доказательство: Используем выражение для      x “ y      в (1.3). Тогда: 

                                  x “ y  =    =   ( x 1 )( y  1)  =  x y x  y  1. 

6.        x  ~  y  =  1  x  y.   

Доказательство:     Легко проверить, что    x ~ y  =  x y   .   Тогда :  

          x  ~  y  =  x y  ( x  1 )( y    1 )  =  x y  x y  x   y  1  =  1  x  y.  

Определение. Полиномом Жегалкина для n  логических переменных называется полином, являющийся суммой константы и различных одночленов, в которые все пере-

менные входят не выше, чем в первой степени: 

                     a      x x … x ,   ( 1 d k d n ) 

причем в каждом наборе   ( i ,   , i )   все   i различны, а суммирование по mod 2  ведется по некоторому множеству таких  не совпадающих наборов.

            Например,    1  x  x x ,      x x x  x x x - некоторые полиномы Жегалкина для двух и трех переменных соответственно.

От формулы алгебры логики всегда можно перейти к формуле алгебры Жегалкина. Для этого нужно заменить основные элементарные функции алгебры логики на соответствующие эквивалентные выражения алгебры Жегалкина (1) - (5), представленные выше.

 В полученной формуле нужно раскрыть скобки и произвести упрощения, используя соотношения (1.4), а также следующие соотношения: x & x  = x и   x·1 = x. Полученное выражение и будет полиномом Жегалкина для данной формулы.

Пример. Найти полином Жегалкина для функции:   f( x, y ) = ( x y )(  x z ). 

Полученное выражение и есть полином Жегалкина.

 

            При нахождении полинома Жегалкина для некоторой формулы алгебры логики можно использовать следующее соотношение, вытекающее из представления дизъюнкции в алгебре Жегалкина:

                           f1  f2 = f1 f2,                                                                           (1.5)

справедливое при   f1f2 = 0. Используем соотношение (1.5) для нахождения полинома Жегалкина в следующих примерах.

Пример. Найти полином Жегалкина для функции:        f( x, y ) =  x y     .

Сделаем следующие преобразования: 

                                      f( x,y )  =   x y     =  x y     =  x y  ( x  1 )( y  1 )  =      

                               =  x y  x y  x  y  1  =    1  x  y  - полиномом Жегалкина.

Пример. Найти полином Жегалкина для функции:       f( x, y )  =  x      z. 

 Сделаем следующие преобразования: 

                              f( x,y )  =  x      z  =  x      z   =  x ( y  1 ) ( x  1 ) z  = 

                             =  x y  x  x z  z  =  x  z  x y  x z. - полиномом Жегалкина.

Теорема. Для любой логической функции существует полином Жегалкина и притом единственный.

Доказательство: Существование полинома доказано вышеприведенным алгоритмом получения полинома из логической формулы. Для доказательства единственности надо показать, что между множеством всех логических функций от n переменных и множеством всех полиномов Жегалкина от n переменных существует взаимно однозначное соответствие.

Полином Жегалкина можно найти методом неопределенных коэффициентов. Рассмотрим этот метод на следующим примере.

Пример. Найти полином Жегалкина для функции заданной векторно:  

                                 f( x,y )  =  ( 0, 1, 1, 0 ).

Составим  таблицу 1.14 задания данной функции.

Таблица 1.14

x	y	f
0	0	0
0	1	1
1	0	1
1	1	0

Полином Жегалкина для функции двух переменных ищем в следующем виде:

f( x, y )  =  a0  a1·x  a2·y a3·xy                                  (1.6)

Для определения коэффициентов полинома нужно подставить значения неизвестных и соответствующее значение функции в (1.6), согласно таблице 1.14.

            Подставляя набор переменных(0,0) в (1.6) получим: 

                                             .      a = 0.

            Аналогично для набора  (0,1) получим: .    a = 1.

     Для набора  (1,0) получим:        a = 1.

            Для набора  (1,1) получим:      a = 0.

Подставляя в (1.6) найденные значения коэффициентов получим искомый полином для данной функции:

f( x, y )  =  x  y.

Замечание. Можно показать, что переменная   x будет фиктивной для некоторой функции тогда и только тогда, когда полином Жегалкина для нее не содержит переменной   x

?) Теорема Поста открывает путь к представлению булевых функций синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицы истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторым термом в сигнатуре Σ, который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?

• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?

  • В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?

• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например, наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

13) Лемма о нелинейной функции.

Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.

Доказательство: Пусть f(x₁,…, x_n ) – нелинейная функция, тогда полином Жигалкина для нее содержит слагаемое, в котором присутствует произведение каких-то переменных x_i*x_j. Пусть для простоты это будет произведение х₁х₂. Произведя группировку слагаемых в полиноме Жегалкина для f относительно x₁х₂, х₁, х₂, функцию f представим в виде f(x₁,…, x_n)=x₁*x₂*h₀(x₃,..,x_n)+ {собрали все слагаемые с x₁*x₂ и вынесли x₁*x₂ за скобки. В скобках осталась сумма h₀(x₃,…,x_n), в которой переменных x₁, x₂ нет} + x₁*h₁(x₃,…, x_n) + x₂*h₂(x₃,…, x_n) + h₃(x₃,…, x_n)

Функция h₀(x₃,…, x_n)≠0, в противном случае многочлен Жигалкина слагаемых с произведением x₁x₂ не имеет, тогда существует набор (a₃,…, a_n) из 0 и1, для которого h₀(a₃,…, a_n)=1. Пусть на этом наборе h₁(a₃,…, a_n)=a h₂(a₃,…, a_n)=b h₃(a₃,…, a_n)=c. Тогда функция g(x₁,x₂)=f(x₁,x₂,a₃,…, a_n)=x₁*x₂+a*x₁+b*x₂+c. Построим функцию h(x₁,x₂) = g(x₁+bx₂+a) = (x₁+b)(x₂+a)+a(x₁+b)+b(x₂+a)+c = x₁*x₂+a*x₁+b*x₂+a*b+a*x₁+a*b+b*x₂+a*b+c = x₁*x₂+a*b+c=x₁*x₂+d, d=a*b+c Если d=0, то h(x₁,x₂)=x₁*x₂, конъюнкция получена. Если d=1, то h(x₁,x₂)=x₁*x₂+1 ⇒ x₁*x₂=⌐h(x₁,x₂), что и требовалось доказать.

16) Релейно-контактные схемы (их часто называют переключательными схемами) широко используются в технике автоматического управления.

 

Под переключательной схемой понимают схематическое изображение некоторого устройства, состоящее из следующих элементов:

 

1)      переключателей, которыми могут быть механические устройства, электромагнитные реле, полупроводники и т.д.;

2)      соединяющие их проводники;

3)      входы в схему и выходы из нее (клеммы, на которые подается электрическое напряжение). Они называются полюсами.

 

Простейшая схема содержит один переключатель Р и имеет один вход А и один выход В. Переключателю Р поставим в соответствии высказывание р, гласящее: - “Переключатель Р замкнут ”. Если р истинно, то импульс, поступающий на полюс А, может быть снят на полюсе В без потери напряжения, то есть схема пропускает ток. Если р ложно, то переключатель разомкнут и схема тока не проводит. Таким образом, если принять во внимание не смысл высказывания, а только его значение, то можно считать, что любому высказыванию может быть поставлена в соответсвие переключательная схема с двумя полюсами (двухполюсная схема).

 

Формулам, включающим основные логические операции, также могут быть поставлены в соответствие переключательные схемы.

 

 

Так, конъюнкции двух высказываний ставится в соответствие схема:

а дизъюнкции - схема:

Так как любая формула может быть записана в ДНФ или КНФ, то ясно, что каждой формуле алгебры логики можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры логики.

Пример 1. По данной формуле составить РКС .

Решение. Упростим данную формулу с помощью равносильных преобразований:

 

 

 

Тогда РКС для данной формулы имеет вид:

 

Пример 2. Упростить РКС:

 

Решение. Составим по данной РКС формулу (функцию проводимости) и упростим ее:

(к последним двум слагаемым применили закон поглощения).

Тогда упрощенная схема выглядит так:

18) Полусумматор — логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, который как правило состоит из двух полусумматоров и логического элемента 2ИЛИ. Представляет собой объединение двух бинарных (двухоперандных) двоичных логических функций: сумма по модулю два - S и разряд переноса при двоичном сложении - C.