15) Метрические задачи

Метрическими называются задачи, связанные с измерением расстояний и углов. В них определяются действительные величины и форма геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям. Решение метрических задач основано на том, что геометрическая фигура, принадлежащая плоскости, параллельной плоскости проекций, проецируется на нее в конгруэнтную ей фигуру (см. аксиомы параллельного проецирования). Поэтому при решении метрических задач широко используются способы преобразования комплексного чертежа, а также теоретические положения, изложенные в теме "Взаимно перпендикулярные прямые и плоскости".

 Проецирование прямого угла.

Теорема: Для того, чтобы прямой угол проецировался ортогонально без искажения, необходимо и достаточно, чтобы, по крайней мере, одна его сторона была параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости.

([AB] [BC]) ([AB] ,[BC] ) [A B ] [B C ]

Рис.6

Дано: ABC=90 [AB] Доказать: A B C =90

Спроецируем [AB] и [BC] на плоскость  .  [AB] [A B ]  [BC] [B C ]

Фигура ABB A  - прямоугольник, следовательно [AB]  плоскости BCC B , так как он перпендикулярен двум пересекающимся прямым этой плоскости (AB BC по условию и AB BB  по построению). Но AB A B , следовательно A B A B  плоскости BCC B , поэтому A B B C , т.е.  A B C =90 .

Обратное утверждение также верно.

По Гордону:

Рис.7

Дано: ABC=90 [AB] Доказать: A B C =90

Пусть [BC] =C Спроецируем [AB] и [BC] на плоскость  .  [AB] [A B ]  [BC] [B C ]

Проведём [DC] [A B ] [DC] [AB], поэтому  BCD=90 На основании теоремы о 3-х перпендикулярах: ( B CD=90 ) ( BCD=90 ) A B C=90 .

Верно также обратное утверждение. Эту теорему применяют при решении задач на определение расстояния от точки до прямой частного положения.

Пример:

Рис.8

Дана горизонталь h и точка С. Надо опустить перпендикуляр из точки C на прямую h. Перпендикуляр из точки C к прямой h образует угол 90  и h H, следовательно прямой угол без искажения проецируется на плоскость H, поэтому из горизонтальной проекции точки C надо опустить перпендикуляр к h1(горизонтальной проекции горизонтали). |C1D1|=|CD|

16 Определение длины отрезка и углов его наклона к плоскостям проекций

.

Рис. 4.6. Определение углов наклона и натуральной величины отрезков

На рис. 4.6 показаны в аксонометрической проекции отрезок АВ и его горизонтальная проекция А₁В₁. Проведя прямую ВВ’, параллельную горизонтальной проекции отрезка А₁В₁ , получим прямоугольный треугольник Δ АВВ’.

Длина отрезка АВ равна гипотенузе этого треугольника, катетами которого являются горизонтальная проекция отрезка А₁В₁ и разность координат z точек А и В (Δz = z_A- z_B).

Как известно, угол наклона прямой к плоскости равен углу между этой прямой АВ и ее проекцией на плоскость (А₁В₁).

Следовательно, угол Δ АВВ’, лежащий против катета Δz, равен углу наклона отрезка АВ и горизонтальной плоскости проекций π₁(угол α°).

.

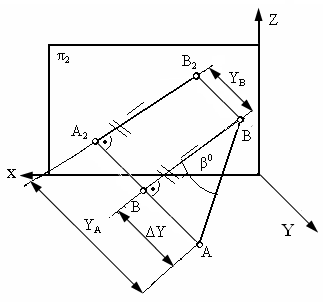
Рис. 4.7. Определение углов наклона и натуральной величины отрезка

Аналогично рассуждая (рис. 4.7), можно показать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А₂В₂ и разность координат Y точек А и В (ΔY =Y_A- Y_B).

Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π₂ (угол β°).

По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А₃В₃ и разность координат Х (Δ Х = Х_А – Х_В) точек А и В. Угол γ° этого треугольника, лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π_3.

На рис. 4.8 показан пример определения длины отрезка АВ и углов наклона его к плоскостям проекций.

17 Предварительное замечание. Параллельность прямых и плоскостей в пространстве и перпендикулярность прямой к плоскости находятся в некоторой зависимости. Именно наличие параллельности одних элементов влечёт за собой перпендикулярность других, и, обратно, из перпендикулярности одних элементов можно сделать заключение о параллельности других. Эта связь между параллельностью и перпендикулярностью прямых и плоскостей в пространстве выражается следующими теоремами.

Теорема. Если плоскость (Р, черт. 18) перпендикулярна к одной из параллельных прямых (АВ), то она перпендикулярна и к другой (CD).

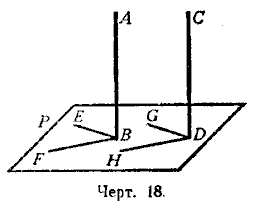
Проведём через точку В на плоскости Р две какие-нибудь прямые ВЕ и BF, а через точку D проведём прямые DG и DH, соответственно параллельные прямым ВЕ и BF. Тогда будем иметь: / АВЕ = / CDG и / ABF = / CDH, как углы с параллельными сторонами. Но углы ABE и ABF прямые, так как АВ _|_ Р, значит, углы CDG и CDH также прямые (§ 18). Следовательно, CD _|_Р  (§ 24).

Обратная теорема. Если две прямые (АВ и СD, черт. 19) перпендикулярны к одной и той же плоскости (Р), то они параллельны.

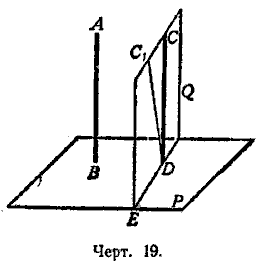
Предположим противное, т. е. что прямые АВ и СD не параллельны. Проведём тогда через точку D прямую, параллельную АВ. При нашем предположении это будет какая-нибудь прямая DС₁ , не сливающаяся с DС. Согласно прямой теореме прямая DС₁ будет перпендикулярна к плоскости Р. Проведём через СD и С₁D плоскость Q и возьмём линию её пересечения DЕ с плоскостью Р. Так как (на основании предыдущей теоремы)  С₁D _|_ Р, то / С₁DE прямой, а так как по условию СD _|_Р, то / СDЕ также прямой. Таким образом, окажется, что в плоскости Q к прямой DЕ из одной её точки D восставлены два перпендикуляра DС и DС₁. Так как это невозможно, то нельзя допустить, чтобы прямые АВ и СD были нe параллельны.

Теорема. Если прямая (ВВ₁, черт. 20) перпендакулярна к одной из параллельных плоскостей (Р), то она перпендикулярна и к другой (Q).

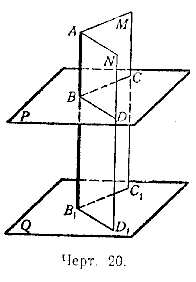
Проведём через прямую ВВ₁ какие-нибудь две плоскости М и N, каждая из которых пересекается с Р и Q по параллельным прямым: одна — по параллельным прямым ВС и В₁С₁, другая—по параллельным прямым ВD и В₁D₁. Согласно условию прямая ВВ₁перпендикулярна к прямым ВС и ВD; следовательно, она также перпендикулярна к параллельным им прямым В₁С₁ и В₁D₁ а потому перпендикулярна и к плоскости Q, на которой лежат прямые В₁С₁ и В₁D₁.

Обратная теорема. Если две плоскости (Р и О, черт. 21) перпендикулярны к одной и той же прямой (АВ), то они параллельны.

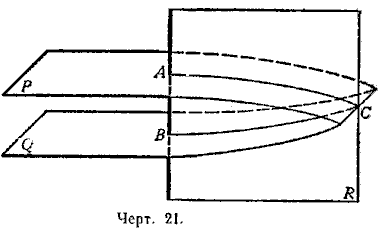
Предположим противное, т. е. что плоскости Р и Q пересекаются. Возьмём на линии их пересечения какую-нибудь точку С и проведём плоскость R через С и прямую АВ. Плоскость R пересечёт плоскости Р и Q соответственно по прямым АС и ВС.  Так как АВ _|_ Р, то АВ _|_ АС, и так как АВ _|_ Q, то АВ _|_ ВС. Таким образом, в плоскости R мы будем иметь два перпендикуляра к прямой АВ, проходящих через одну и ту же точку С, перпендикуляры АС и ВС. Так как это невозможно, то предположение, что плоскости Р и Q пересекаются, неверно. Значит, они параллельны.