Задача 3.123.

Конденсатор емкости C1=1,0 мкФ, заряженный до напряжения U=110B, подключили параллельно к концам системы из двух последовательно соединенных незаряженных конденсаторов, емкости которых C2=2,0 мкФ и C3=3,0 мкФ. Какой заряд протечет по соединительным проводам?

Решение:

З аряды на конденсаторах после подключения равны между собой:

Заряд, протекший после соединения, равен заряду на одном из конденсаторов;

О твет:

Задача 3.126

Н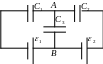 айти разность потенциалов φ(А)-φ(В) между точками схемы

Решение:

Р ассмотрим два контура для каждого из источников:

Для точки А запишем также закон сохранения заряда:

г де

Р ешаем систему уравнений и получаем:

Откуда

Задача 3.133

Конденсатор емкости С₁ = 1 мкФ, предварительно заряженный до напряжения U = 300 B, подключили параллельно к незаряженному конденсатору С₂=2 мкФ. Найти приращение электрической энергии этой системы E к моменту установления равновесия

Решение

Т. к. в начальный момент времени заряжен только первый конденсатор, то энергия системы в начальный момент времени выражается формулой:

; (1)

Заряд первого конденсатора определяется по формуле:

; (2)

Равновесие система достигнет, когда сравняются напряжения на конденсаторах:

; (3)

Т. к. q₀=q₁+q₂, то, выражая отсюда q₂ и подставляя полученное выражение в (3) :

; (4)

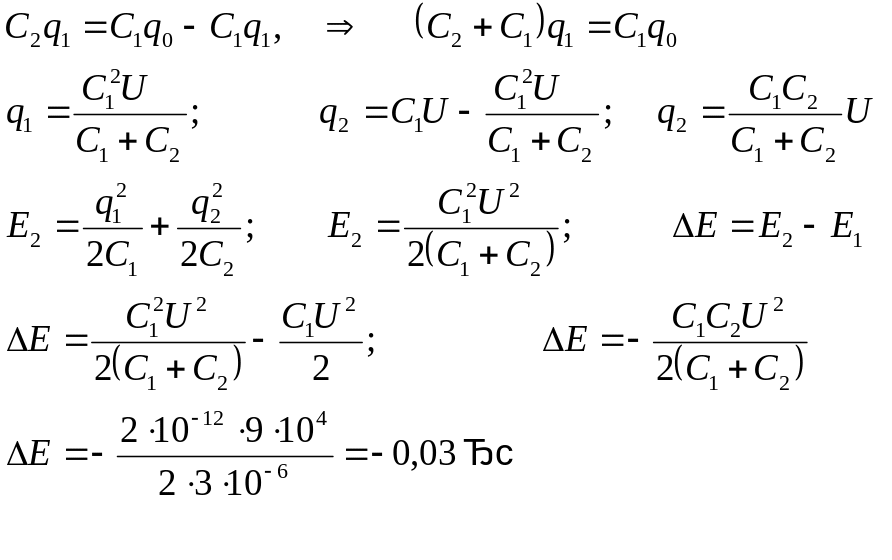
Ответ: E = -0,03 Дж.

Задача 3.161.

З азор между обкладками плоского конденсатора заполнен стеклом с удельным сопротивлением =100ГОмм. Емкость конденсатора C=4,0нФ. Найти ток утечки через конденсатор при подаче на него напряжения U=2,0кВ.

Решение:

Н айдем активное сопротивление R конденсатора.

Г де, в нашем случае, l ­— расстояние между обкладками конденсатора, а S — площадь пластин конденсатора находим из формулы для плоского конденсатора:

Получаем для R:

И з закона Ома находим ток утечки:

О твет:

Задача № 3.170.

К онденсатор емкости C=400пФ подключили через сопротивление R=650 Ом к источнику постоянного напряжения U₀. Через сколько времени напряжение на конденсаторе станет U=0,90U₀?

Р ешение:

По правилу Кирхгофа запишем уравнение:

Это дифференциальное уравнение с разделяющимися переменными.

п роинтегрировав, получаем:

Константу C определяем из начальных условий:

В начальный момент конденсатор не заряжен: t=0, q=0 

Получаем: , или для напряжения на конденсаторе:

; зная что U=0.90U₀ получаем:

логарифмируя, приходим к ответу:

Ответ: .

Задача 3.173.

А мперметр и вольтметр подключили последовательно к батарее с ЭДС  = 6.0 В. Если параллельно вольтметру подключить некоторое сопротивление, то показание вольтметра уменьшается в  = 2.0 раза, а показание амперметра во столько же раз увеличивается. Найти показание вольтметра после подключения сопротивления.

Решение:

Запишем закон Ома для схемы до и после подключения сопротивления (1), (2)

  = I1Ra + I1Rv (1)

  = I2Ra + I2(Rv+R)/(Rv+R) (2)

 U1=I1Rv (3)

 U2=I2(Rv+R)/(Rv+R) (4)

 U2 = U1 (5)

 I1 = I2 (6)

 U2=?

Решаем систему и находим U2 :

(1): /I1 = Ra + Rv , (2): /I2 = Ra+ (Rv+R)/(Rv+R)  /I2  (-1) = Rv - (Rv+R)/(Rv+R) (*)

(3), (4): U1/U2 = I1/I2  (Rv+R)/(Rv+R)  (5),(6): ² = (Rv+R)/R  (*): Rv = R(² - 1) (**)

(4),(*): U2 = ( - 1)( Rv(Rv+R)/(Rv+R) – 1 ) = ( -1)(Rv/R) = (**): ( - 1)/ (² - 1) =  / (+1)

Ответ: U2 =  / (+1); U2=2.0 В.