Задачи по физике Задача 3.8

Тонкое полукольцо радиуса r=20 см заряжено равномерно зарядом q=0,70 нКл.

Найти модуль напряженности в центре кривизны этого полукольца.

Решение:

Р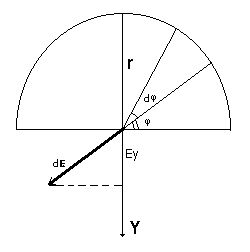 азобьем полукольцо на малые элементы , видимые под углом d. Один элемент создает напряженность dE.

В проекции на ось Y:

( 1), где

П одставляя полученное значение для dq в (1), получим:

Интегрируя по углу, получим:

Ответ:

кВ/м.

Задача 3.13

Находящийся в вакууме тонкий прямой стержень длины 2a заряжен равномерно

зарядом q. Найти модуль напряженности электрического поля как функцию расстояния r от центра стержня до точки прямой,

1. перпендикулярной к стержню и проходящей через его центр;

2. совпадающей с осью стержня при r>a.

Решение:

а ) На стержне на расстоянии x от центра стержня выберем элемент dx. Тогда на расстоянии h от центра стержня этот элемент создает напряженность

, где .

Или в проекции на ось X:

.

Интегрируя, получим значение напряженности, создаваемой всем стержнем:

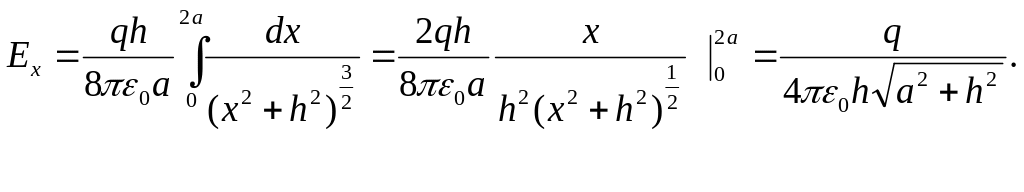
При h>>a получим выражение для напряженности:

б)

Н а расстоянии х от края стержня выберем элемент dx. На расстоянии h от правого края стержня этот элемент создает напряженность

Интегрируя, получим:

Учитывая, что h=r+a, получим:

При h>>a

Ответ: a)

б)

При h>>a в обоих случаях

Задача 3. 16

Сфера радиуса R заряжена с поверхностной плотностью =aR, где а - постоянный вектор, R-радиус вектор точки сферы, относительно ее центра. Найти напряженность в центре сферы.

Р ешение

=ar;  =arcos ; sin =cos;

В ыделим на сфере эл. площадку ds ;

dq= ds*  ;

тогда E:

О твет:

Задача 3.22

Шар радиуса R имеет заряд, объемная плотность которого зависит от расстояния R

до его центра как =₀*(1-r/R), где ₀  постоянно.

Найти

а) Модуль напряженности, как функцию от r

б) E max и соответствующий ему r max

Решение

а) r>=R если r>R то заряд сферы можно рассматривать , как точечный заряд в ее центре:

E =1/4* q/r*r;

r<R

е сли точка находится внутри сферы,то поле в создается только сферой радиуса r, тогда заряд сферы радиуса r:

а поле:

б ) Em:

достигает максимума ,при r равном 2R/3;

О твет:

З адача 3.29.

Вычислить разность потенциалов (U) т. 1 и 2, если т. 2 находится дальше от заряженной нити, чем 1, в  раз.

 = 2 ,  = 0,4 мкКл / м.

Решение

Н апряженность эл. поля, создаваемого бесконечно длинной заряженной нитью в зависимости от расстояния r.

Ответ: U = 5 kB.

Задача 3.31.

Полусфера радиуса R заряжена с поверхностной плотностью , найти потенциал  и напряженность эл. поля Е в центре полусферы.

Решение

Н ужно просуммировать проекции вектора Е только на вертикальную ось OZ:

Задача 3.34

Заряд q распределен равномерно по объему шара радиуса R . Полагая диэлектрическую проницаемость всюду равной единице найти потенциал в центре шара.

Решение:

Найдем заряд в единице обьема шара:

Заряд сферического слоя:

Интегрируя по R_слоя :

О твет:

Задача 3.54

Два точечных заряда q и –q расположены на расстоянии L друг от друга и на одинаковом расстоянии L/2 от проводящей плоскости с одной стороны её. Найти модуль электрической силы действующей на каждый заряд.