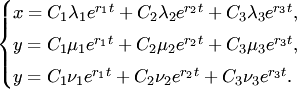28. Системы ду, основные понятия (нормальная система, теорема Коши…)

решение многих прикладных задач м требовать нахождения сразу нескольких неизвестных ф-ий. Для этого необходимо располагать таким же числом уравнений. Если каждое из этих уравнений явл-ся дифференциальным, т.е. содержит неизвестную ф-ию и её производную, независимую прм, то речь идет о системе ДУ, кот можно записать в виде:

если разрешить каждое ур этой системы относ-но производной, то получим нормальную систему ДУ, при этом предполагается, что число уравнений=числу искомых ф-ий.

Решением этой системы наз-ся совокупность ф-ий у₁, у₂, …, у_n, удовлетворяющих каждому из уравнений системы. Начальные условия для системы y₁(x₀)=y₁⁰, y2(x₀)=y₂⁰, y_n(x₀)=y_n⁰.(2)

На системы ДУ обобщается постановка задачи Коши для одного уравнения: найти решение системы (1), удовлетворяющее нач условиям (2).

Условие существования и единственности решения задачи Коши описывает теорема Коши: если в системе (1) все ф-ии f_i(x,y1,y2,…,yn) непрерывны вместе со всеми своими частными производными по y_i в некоторой области D (n+1)-мерного пространства, то в каждой точке M₀(x₀,y₁⁰,y₂⁰,…,y_n⁰) этой области сущ-ет и при том единственное решение y₁=φ₁(x), y₂= φ₂(x),…, yn= φ_n(x) системы, удовлетвор нач условиям (2) в окрестности т х₀.

Если менять т М₀ в области D, т.е. нач условия, то получим бесчисленное множество решений, которые можно записать в виде решения зависящего от n произвольных постоянных: y1=φ1(x,c1,c2,…,c_n), y2= φ2(x,c1,c2,…,c_n),…,y_n= φ_n(x,c1,c2,…,c_n). Это решение явл общим, если по заданным н.у. можно однозначно определить пост с1,с2,…, с_n из системы уравнений:

частным решением наз-ся решение, которое получается из общего при конкретных значениях постоянных с1, с2, …, с_n.

К системе ДУ 1ого порядка во многих случаях сводится уравнения и системы уравнений высших порядков. Например: y”’=f(x,y,y’,y”). обозначим y’и y” ч/з u и v соответственно. Тогда уравнение можно заменить системой

29. Достаточные и необходимые условия существования и единственности решения задачи Коши для нормальной системы. Понятие об общем и частном решениях.

Нормальную систему ДУ можно получить в результате разрешения относительно производной системы ДУ, состоящей из n уравнений и имеющей вид

Нормальная система имеет вид:

(1)

Предполагается, что число уравнений равно числу искомых функций.

Решение системы (1) – совокупность функций ,… , удовлетворяющих каждому из уравнений этой системы.

Начальные условия для системы (1) имеют вид:

(2)

Условия существования и единственности решения задачи Коши описывает т. Коши:

Если в системе (1) все функции 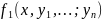непрерывны вместе со своими частными производными по некоторой области D ((α+1) – мерного пространства), то в каждой точке этой области существует единственное решение системы, удовлетворяющее начальным условиям (2) окрестности точки .

Если менять точку в области D (т.е. начальные условия), получим бесчисленное множество решений, которое можно записать в виде решения, зависящего от n производных постоянных

Это решение является общим, если по заданным начальным условиям можно однозначно определить постоянные из системы уравнений

Частным решением называется решение, которое получается из общего при конкретных значениях постоянных .

Следует заметить, что к системам ДУ первого порядка во многих случаях сводится уравнения и системы уравнений высших порядков.

Пример:

Обозначим и запишем системы

Аналогичное истолкование допускает любое другое ДУ или система уравнений.

30) СВЯЗЬ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ И СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Задача Коши для любого дифференциального уравнения n–го порядка, записанного в нормальной форме,

y⁽ⁿ⁾= F(x, y, y ', y '', … , y⁽ⁿ⁻¹⁾ ) = 0,   y(x₀) = y₀,   y '(x₀) = y₁,   y ''(x₀) = y₂, … , y^{(n − 1)} (x₀) = y_{n− 1} ,

может быть сведена к задаче Коши для системы дифференциальных уравнений n– го порядка.

Обозначим

z₁(x) = y(x),   z₂(x) = y'(x),   z₃ (x) = y ''(x), … , z_n( x) = y ^{(n − 1)}(x ).

Тогда

F(x, y, y ', y '', … , y⁽ⁿ⁻¹⁾) ≡ F(x, z₁, z₂, z₃, … , z_n)  

и задача Коши для уравнения записывается в виде задачи Коши для системы

Эта задача в векторной форме записывается в виде:

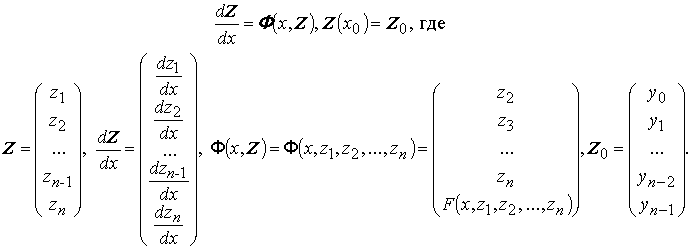
31)Однородные системы

Однородной системой линейных уравнений называется система вида:

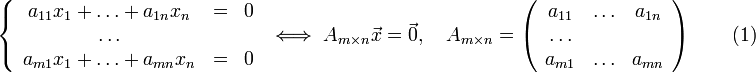
	Теорема (о линейном решении однородных систем). Пусть — решения однородной системы (1), — произвольные константы. Тогда также является решением рассматриваемой системы.
	Пусть дана однородная система (1), тогда набор векторов размера называется фундаментальной системой решений (ФСР) (1), если: — решения системы (1); линейно независимы; . Теорема (о ФСР). Пусть ранг основной матрицы , где — число переменных системы (1), тогда: ФСР (1) существует: ; она состоит из векторов; общее решение системы имеет вид . Замечание: Если , то ФСР не существует.

Неоднородные системы

Неоднородной системой линейных уравнений называется система вида:

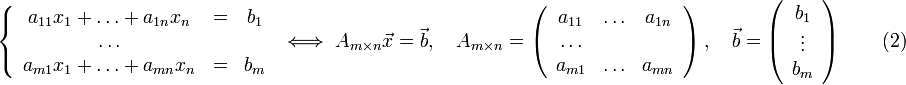
— её расширенная матрица.

Линейная зависимость функций. Определитель Вронского, его свойства. Фундаментальная система решений.

Средством изучения линейной зависимости системы функций является так называемый определитель Вронского (Вронскиан)

Для 2-х дифференциальных уравнений y₁=y₁(x) и y₂=y₂(x) определитель Вронского имеет вид:

W(x)=

Теорема 2.2.: если дифференциальные функции y₁(x) и y₂(x) линейно зависимы на (a;b), то составленный из них определитель Вронского на этом интервале тождественно равен 0

Т.к. y₁(x) и y₂(x) линейно зависимы, то в равенстве: α₁y₁(x)+α₂y₂(x)=0 α₁ или α₂ ≠0

Пусть α₁≠0, тогда y₁=-(α₂/α₁)y₂

Поэтому для всех x принадлежащих (a;b): W(x)= = =0

что и требовалось доказать

Теорема 2.3. Если решения y₁(x) и y₂(x) уравнения (2.1) линейно независимы на интервале (a;b), то составленный из них определитель Вронского отличен от 0 на этом интервале

замечание: из теорем 2.2. и 2.3. следует, что W(x)≠0 ни в одной точке (a;b) т.т.т., когда частные решения линейно независимы.

совокупность любых двух линейно независимых на интервале (a;b) частных решений y₁(x) и y₂(x) уравнения (2.1) определяют фундаментальную систему решений этого уравнения: любое произвольное решение м.б. получено как комбинация y=α₁y₁(x)+α₂y₂(x). Теперь можно сказать, при каких условиях функция y=C₁y₁(x)+C₂y₂(x) будет общим решением.

32)Рассмотрим этот метод в применении к системе трех линейных дифференциальных уравнений:

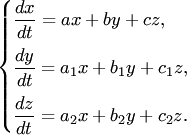(3)

Решение системы (3) ищем в виде

(4)

Подставляя (4) в (3) и сокращая на , получаем систему уравнений для определения и

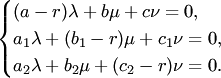(5)

Система (5) имеет ненулевое решение, когда ее определитель равен нулю,

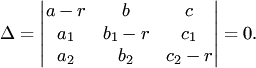(6)

Уравнение (6) называется характеристическим.

А. Пусть корни и характеристического уравнения — вещественные и различные. Подставив в (5) вместо число и решив систему (5), получим числа и . Затем положим в (5) и получим числа и, наконец, при получим и . Соответственно трем наборам чисел и получим три частных решения

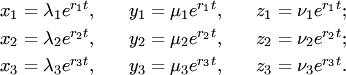
Общее решение системы (3) имеет вид