4. Задача Коши для ду 1-го порядка. Механическое истолкование ду 1-го порядка и его решений.

Во многих задачах, которые приводятся по ДУ 1-го порядка, требуется найти решение при заданном начальном значении независимой переменной. Такая задача называется задачей Коши.

y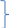 ^’=f(x)

начальные данные x₀ , y₀

y(x₀)=y₀

y=y(x, x₀, y₀)-решение задачи Коши

Геометрически речь идет о нахождение интегральной кривой проходящей через точку M₀ (x₀,y₀)

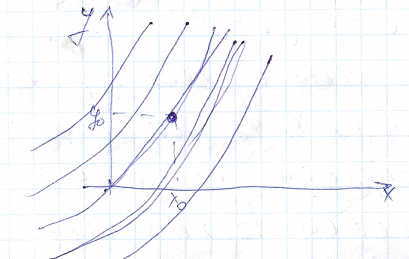
Большое значение для теории диф. ур-я и её приложений имеет вопрос о существование решении задачи Коши и о единственности этого решения. Задача Коши имеет единственное решение, если можно указать такую окрестность точки x₀ , что |x-x₀|<h, в ней определенное решение y=y(x, x₀, y₀) и не существует другого решения y=y₁(x, x₀, y₀). Если такое решение существует, то говорят, что единственность решения задачи Коши нарушена.

Механическое истолкование:

Скорость движения есть функция f(t,x)

V=f(t,x) dx/dt=f(t,x)

Любое решение x=xt представляет закон движения

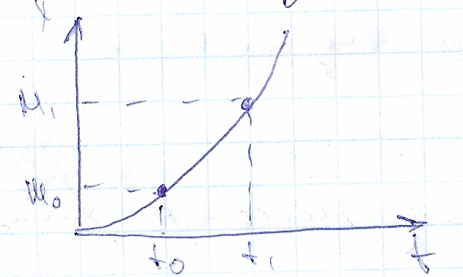
Отрезок MM₁ – траектория x(t₀)=M₀

Есть частные случаи:

1. Когда правая часть не зависит от х

dx/dt=f(t)

2. Когда правая часть не зависит от t

dx/dt=f(x)

если правая часть р/м ур-я обращается в нуле, при x=x₀ при всех р/м значениях времени t, так что скорость данной точки равна нулю f(t,x₀)=0

5. Теорема о существовании единственности решения ду 1-го порядка. Случай линейного ду 1-го порядка: выбор начальных данных и интервал существования решения.

Р/м линейное ур-е dy/dx + p(x)y=a(x)

Функции Q(x), p(x) непрерывны в интервале ав, для того чтобы применить теорему Пикара нужно переписать ур-е в виде: dy/dx=Q(x)-p(x)y=f(x)

На выбор начального значения y₀ никаких ограничений налагать не надо, поскольку f(x,y) является линейной ф-ей, поэтому она будет непрерывна на (x₀,y₀), если x₀ лежит в интервале непрерывной ф-ции р(х) и Q(x). Частная производная равна –р(х). Т.О. для линейного ур-я y₀ можно выбирать произвольно, а x₀ можно брать любой из [a,b], в котором Q(x), p(x) непрерывны. При таких начальных данных решение уравнения существует и единственно.

Замечание: линейное ур-е обладает преимущество перед линейным ур-ем в отношении выбора начальных данных и в отношение интервала существования решения.

6) Метод последовательных приближений решения ду 1-ого порядка.

Пусть требуется найти решение дифференциального уравнения

(1)

удовлетворяющее начальному условию

(2)

Будем предполагать, что в некотором прямоугольнике с центром в точке для уравнения (1) выполнены условия а) и б) теоремы существования и единственности решения задачи (1)-(2).

Решение задачи (1)-(2) может быть найдено методом последовательных приближений, который состоит в следующем.

Строим последовательность функций, определяемых рекуррентными соотношениями

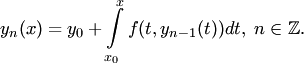(3)

В качестве нулевого приближения можно взять любую функцию, непрерывную в окрестности точки , в частности — начальное значение Коши (2). Можно доказать, что при сделанных предположениях относительно уравнения (1) последовательные приближения сходятся к точному решению уравнения (1), удовлетворяющему условию (2), в некотором интервале , где

(4)

Оценка погрешности, получаемой при замене точного решения n-м приближением , даётся неравенством

(5)

где . Применяя метод последовательных приближений, следует остановиться на таком , для которого не превосходит допустимой погрешности.

7) Понятие об общем, общем в форме Коши,частном и особом решениях ДУ 1-го порядка.

Р/м уравнение первого порядка в нормальной форме .

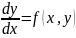Пусть D некоторая область на плоскости XY через каждую точку, которой проходит одна и только одна интегральная кривая. Функция 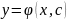определенная в некоторой области измененных переменных x и c и непрерывно дифференцируемая относительно Х называется общим решением рассматриваемого уравнения в области D, если она удовлетворяет следующим условиям:

1. Равенство в уравнении разрешимо в области D относительно произвольной постоянной С.

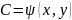
2. Функция 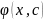является решением исходного уравнения при всех значениях произвольной постоянной С доставляемых формулой

Знание общего решения дает решить задачу Коши с любыми начальными данными 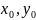из области D за счет выбора соответствующего значения произвольной постоянной С.

Запись общего решения 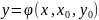называется общим решением в форме Коши.

Решение y=y(x) в каждой точке которого сохраняется единственность решения задачи Коши, называется частным решением.

Решение y=y(x) в каждой точке которого нарушается единственность решения задачи Коши, называется особым решением.

8) Построение ДУ 1-го порядка заданного семейства кривых.

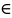Предположим, что уравнение Ф(x,y,c)=0 разрешимо относительно у: у=у(х,с) х (а,b) подставим это значение в уравнение семейства кривых :

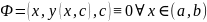
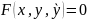
Полученное ДУ называется ДУ заданным семейством кривых.

Семейство кривых Ф(x,y,c)=0 обычно является общим интегралом уравнения следовательно, каждая кривая является частным интегралом уравнения

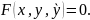
Полученное ДУ может содержать также и свои решения не входящие в семейство кривых Ф(x,y,c)=0.