Необходимость.
Т.к.
,
то выбираем допустимое решение
Рассмотрим
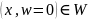
Т.к.
,
то
Достаточность.
Пусть вспомогательная задача решена и для нее построена симплекс таблица:
Все относительные оценки неотрицательные, т.к. таблица оптимальная
, получаем НР1
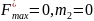
Все
искусственные переменные исключены из
базиса, то вычеркиваем все столбцы,
соответствующие переменны и дописываем
новую строку
по тем же правилам
-
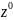
f
Получена начальная симплекс таблица задачи.
Среди
Выбрав любой ненулевой элемент сделать шаг жордановых исключений
(случаи
2,3) тем самым получаем разрешимость
,
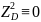исходная матрица имеет ранг
Система уравнений задачи (I) линейно зависима, поэтому вычёркиваем столбцы и строки, соответствующие искусственным переменным, чтобы построить начальную симплекс таблицу задачи (I). Дальше то же, что и в пункте 2
ПРИМЕР
Построим каноническую форму задачи:
Строим вспомогательную задачу
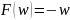
Случай 1
|
|
|
|
|
|
|
- |
1/3 |
1/3 |
|
17/3 |
|
- |
5/3 |
-1/3 |
|
13/3 |
|
- |
2/3 |
-1/3 |
|
1/3 |
|
|
|
|
|
|
|
- |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
1 |
0 |
|
6 |
6/1 |
0 |
|
-1 |
1 |
0 |
|
4 |
- |
-1 |
|
3 |
2 |
-1 |
|
1 |
1/3 |
|
|
|
|
|
|
|
|
|
|
-3 |
-2 |
1 |
|
-1 |
|
|
|
|
|
|
|
|
|
Строим начальную таблицу
|
|
5 |
0 |
|
|
|
|
|
|
|
|
0 |
|
1/3 |
1/3 |
|
17/3 |
0 |
|
5/3 |
-1/3 |
|
13/3 |
2 |
|
2/3 |
-1/3 |
|
1/3 |
|
|
|
|
|
|
|
|
-11/3 |
-2/3 |
|
2/3 |