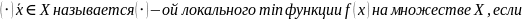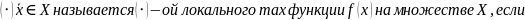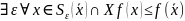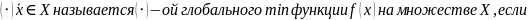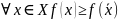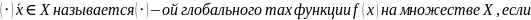- •Пример прикладных задач Задача 1. Производственная задача
- •Задача 2. О строительстве зрительного зала
- •Задачи нелинейного программирования
- •Линейное программирование
- •Свойства задач линейного программирования
- •Симплекс метод
- •Формальное описание симплекс метода
- •Правило одного шага Жорданого исключения
- •Метод искусственного базиса
- •Необходимость.
- •Теория двойственности в линейном программировании
- •Одновременное решение прямой и двойственной задачи
Математическое программирование
Пример прикладных задач Задача 1. Производственная задача
Фирма хочет наладить производство некоторых товаров с тем, чтобы от их реализации получалась max прибыль с учетом ограниченности ресурсов
Введем обозначения:
n – число различных товаров
m – число различных товаров
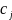 – прибыль от j-го товара
(
– прибыль от j-го товара
(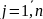 )
)
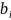 – количество i-го ресурса
(
– количество i-го ресурса
(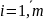 )
)
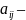 расход
i-го ресурса при производстве
единицы j-го товара
расход
i-го ресурса при производстве
единицы j-го товара
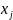 – объем выпускаемого j-го
товара
– объем выпускаемого j-го
товара
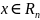 – производственный план
– производственный план
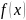 – прибыль
– прибыль
 – необходимо максимизировать
– необходимо максимизировать
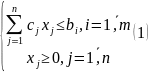
 – количество единиц i-го
ресурса, которого будет реализовано в
связи с планом
– количество единиц i-го
ресурса, которого будет реализовано в
связи с планом

Построенная математическая модель представляет собой задачу линейного программирования.
Задача 2. О строительстве зрительного зала
Необходимо спроектировать зрительный зал в здании, имеющем форму полу эллипсоида max объема в форме прямоугольника, боковые стены которого должны быть плоскостям симметрии полу эллипсоида.
a, b, c – размеры полу эллипсоида
x – вершина прямоугольника (принадлежащая полу эллипсоида)
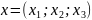
Тогда объем
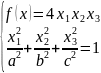
2е т.к. вершина должна лежать на полу эллипсоиде
Мы построили задачу типа классических задач Лагранжа – задача нелинейного программирования
Общая задача математического программирования
при ограничениях:
|
|
ОПРЕДЕЛЕНИЕ
|
|
ОПРЕДЕЛЕНИЕ
|
|
ОПРЕДЕЛЕНИЕ
|
|
ОПРЕДЕЛЕНИЕ
|
|
ОПРЕДЕЛЕНИЕ Оптимальное решение – глобальный экстремум |
|
Под стандартной формой задачи математического программирования понимают
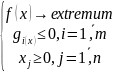
Под канонической формой понимают
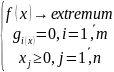
Правила перехода от одной формы к другой
Связь между типами экстремумов
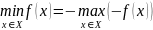
Если «
 »,
то умножив на (-1) поменяем тип неравенства
на «
»,
то умножив на (-1) поменяем тип неравенства
на «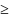 »
»Если ограничение имеет форму неравенства, вводим дополнительную переменную и заменяем неравенство на равенство
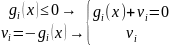
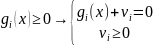
Переход от равенств к неравенствам:
1
вариант.
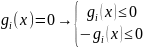
2 вариант. За счет выражения одной переменной через другую
Классификация задач математического программирования
Задачи линейного программирования (ЗЛП)
имеет вид


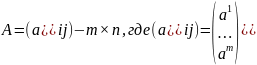
Задачи выпуклого программирования (ЗВП)

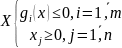
Необходимо, чтобы

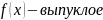
-
ОПРЕДЕЛЕНИЕ
Множество X называется выпуклым, если
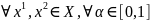
 – выпуклая комбинация 2-х точек (при
фиксированном
– выпуклая комбинация 2-х точек (при
фиксированном
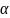 )
)
Все выпуклые
комбинации 2х точек образуют выпуклую
оболочку, натянутую на 2
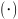
-
ОСНОВНОЕ СВОЙСТВО
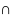 выпуклых множеств всегда выпукло
выпуклых множеств всегда выпуклоОПРЕДЕЛЕНИЕ
Функция
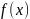 ,
определенная на выпуклом множестве
,
определенная на выпуклом множестве
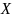 ,
называется выпуклой,
если
,
называется выпуклой,
если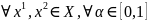
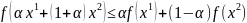
-
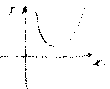
ПРИМЕР
Если – выпуклая, то функция
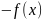 – тоже выпуклая
– тоже выпуклаяЦЕНТРАЛЬНОЕ СВОЙСТВО
 локальный
локальный
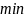 выпуклой функции является глобальным
выпуклой функции является глобальным( локальный
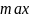 вогнутой функции является глобальным)
вогнутой функции является глобальным)
Среди задач выпуклого программирования выделяются задачи выпуклого квадратичного программирования (ЗВКП).
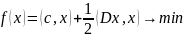
 ,
где D-матрица 2-ых
частных производных
,
где D-матрица 2-ых
частных производных

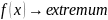
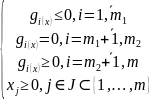
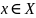 – множество допустимых решений задачи
– множество допустимых решений задачи