6.5.7 Частный случай лоду второго порядка. Формула Лиувилля-Остроградского
Рассмотрим ЛОДУ второго порядка
|
(6.33) |
,
.
Коэффициенты , непрерывны на промежутке . Пусть и – фундаментальная система решений уравнения (6.33). Определитель Вронского этих функций
,
а
его производная
.
Так как
и
удовлетворяют ЛОДУ (6.33), то нетрудно
проверить, что
.
Разделяя переменные и интегрируя это уравнение, получим
.
Откуда
.
Подставляя
в это равенство
,
получим формулу Луивилля-Остроградского:
|
(6.34) |
.
Замечание 1 Формула Луивилля-Остроградского справедлива и для уравнения порядка n.
Замечание 2 Из формулы Луивилля-Остроградского непосредственно следует свойство вронскиана, составленного из n решений ЛОДУ порядка n (см. замечание п. 6.5.3):
либо вронскиан равен нулю на всём промежутке , в этом случае функции линейно зависимы;
либо вронскиан не обращается в нуль ни в одной точке промежутка , в этом случае функции линейно независимы.
Замечание 3
Линейное дифференциальное уравнение
(6.33) можно преобразовать в дифференциальное
уравнение первого порядка (уравнением
Риккати) с помощью подстановки
.
В результате получим уравнение
.
Замечание 4 Уравнение (6.33) обладает важным свойством: если известно одно частное решение уравнения (6.33), то можно определить с помощью интегрирования второе частное решение этого уравнения, линейно независимое от первого, т.е. найти общее решение уравнения. Действительно, пусть некоторое частное решение уравнения (6.33). Для получения второго частного решения воспользуемся формулой Луивилля-Остроградского.
Запишем
её в виде
,
и разделим обе части на
,
получим
или
.
Интегрируя обе части последнего равенства и затем умножая на , получим искомую функцию
|
(6.35) |
.
Полагая
(а это означает, что вронскиан отличен
от нуля в некоторой точке), получим
решение уравнения (6.33) линейно независимое
от
.
Пример 73 Рассмотрим уравнение
,
,
.
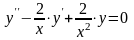Нетрудно
проверить, что функция
является решением этого уравнения.
Воспользуемся формулой (6.35) для нахождения
второго частного решения.
.
Общее решение получаем, как линейную комбинацию
.
6.5.8 Линейные неоднородные дифференциальные уравнения. Структура общего решения. Метод вариации произвольных постоянных
Рассмотрим неоднородное линейное дифференциальное уравнение (ЛНДУ)
|
(6.35) |
,
,
которое
можно записать с помощью линейного
дифференциального оператора в виде
Коэффициенты
,
…,
и правую часть
предполагаем непрерывными на промежутке
,
так что для уравнения (6.35) имеет место
теорема существования и единственности
решения.
В п. 6.5.2 рассматривались свойства линейного дифференциального оператора. Проведём ещё несколько свойств этого оператора.
Свойство
1 Если
функция
является решением однородного уравнения
,
а функция z
– частное решение неоднородного
уравнения
,
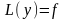то их сумма
является решением неоднородного
уравнения
.
Действительно,
если
и
,
то
,
что и утверждается.
Свойство 2 Если правая часть неоднородного уравнения (6.35) есть сумма двух функций, т.е.
,
то
частное решение такого уравнения можно
получить как сумму частных решений
аналогичных уравнений с правыми частями
и
.
Доказательство этого свойства следует из линейности оператора L.
Свойство
3 Если
уравнение
(
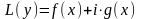– мнимая единица), где
и
– действительные функции, имеет решение
,
то действительная часть решения
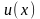и мнимая часть решения
являются соответственно решениями
уравнений
и
.
В частности, если уравнение однородное , то и действительная часть и мнимая часть являются решениями однородного уравнения.
Доказательство.
Пусть
.
Тогда
.
Из равенства комплексных чисел следует,
что мнимые и действительные их части
равны, т.е.
и
.
Структура общего решения ЛНДУ раскрывается в следующей теореме.
Теорема.
Общее решение
уравнения
,
равно сумме общего решения соответствующего
однородного уравнения
и какого-нибудь частного решения
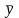неоднородного уравнения.
Доказательство.
Пусть
,
фундаментальная система решений
однородного уравнения, тогда общее
решение этого уравнения
,
где
– произвольные постоянные (п. 6.5.5). Надо
доказать, что функция
является общим решением неоднородного уравнения . Дальнейшие рассуждения почти дословно совпадают с рассуждениями в доказательстве теоремы о структуре общего решения однородного уравнения (п. 6.5.5).
Пример 74 Рассмотрим дифференциальное уравнение
.
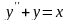Нетрудно
проверить, что функции
и
образуют фундаментальную систему
решений однородного уравнения
(проверьте, что эти функции являются
решениями и линейно независимы). Поэтому
общее решение однородного уравнения
имеет вид
,
где
,
– произвольные постоянные. Кроме того,
функция
является частным решением заданного
неоднородного уравнения. Из доказанной
теоремы следует, что общее решение
заданного уравнения имеет вид
.
Если общее решение однородного уравнения известно и имеет вид
,
то нахождение общего решения неоднородного уравнения можно осуществить методом вариации произвольных постоянных.
Продемонстрируем этот метод для случая уравнения второго порядка
|
(6.37) |
,
Пусть
и
– фундаментальная система решений
соответствующего однородного уравнения
,
и
общее решение этого уравнения
,
где
и
– произвольные постоянные.
Идея
метода вариации произвольных постоянных
состоит в том, что решение неоднородного
уравнения ищется в том же виде, но при
этом считаем постоянные
и
некоторыми функциями от х
,
,
т.е. решение ищем в виде
|
(6.38) |
.
Подчиним функции , следующим условиям:
|
(6.39) |
Эта система называется системой Лагранжа.
Определителем
системы (6.39) является вронскиан функций
,
,
которые линейно независимы. Следовательно,
вронскиан отличен от нуля и система
всегда имеет единственное решение
,
.
Интегрируя функции, найденные в результате
решения системы, и подставляя результат
в (6.38), получим искомое решение неоднородного
уравнения. Непосредственная подстановка
функции (6.38) в исходное уравнение (6.37)
показывает, что при выполнении условий
(6.39) уравнение удовлетворяется.
Замечание. Метод вариации произвольных постоянных применим в случае уравнения порядка n . При этом система Лагранжа принимает вид
где , , …, – фундаментальная система решений однородного уравнения .
Пример 75 Найти общее решение уравнения
.
Решение:
В конце п. 6.5.6 найдено, что фундаментальная
система решений соответствующего
однородного уравнения
,
.
Решение заданного уравнения ищем в виде
.
Система Лагранжа в этом случае имеет вид
из
которой находим
,
.
Интегрируем
последние равенства
,
,
где
,
– постоянные.
Общее решение заданного уравнения
.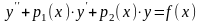