4°. Уравнение Клеро:

Делаем замену тогда

Далее

Уравнение распадается на два:

Из первого уравнения следует, что p=c и, значит, Это семейство прямых линий является общим решением.

Уравнение вместе с уравнением доставляют ре-шение уравнения Клеро в параметрической форме:

которое обычно является особым решением, причем оно заведомо будет особым, если сохраняет знак.

 

П. 11.9

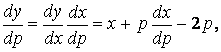
Делаем замену тогда Уравнение распадается на два: Общее решение: Из второго уравнения находим:

Исключая параметр p, получаем особое решение в явном виде:

 

П. 11.10

Делаем замену тогда

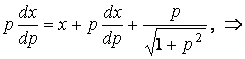
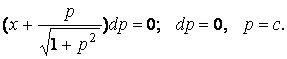Общее решение: Далее,

Исключая из этих урав-нений параметр p, находим особое решение в виде

Задача коши.

Справедлива следующая теорема существования и единственности решения задачи Коши. Если правая часть уравнения y⁽ⁿ⁾) = f(x, y, y', y'', ..., y^(n-1)) и ее частные производные по переменным y, y', y'', ..., y^(n-1) непрерывны в области G Rⁿ+1, то для любой точки (x₀, y₀, y_0,1, y_0,2, ..., y_0,n-1) из G на некотором интервале (x₀-h, x₀+h) существует единственное решение y(x) уравнения, удовлетворяющее начальным условиям.

Опр. Общим решением (общим интегралом) уравнения называется такое соотношение , что: 1. Любое решение этого соотношения относительно y (для набора постоянных C₁, C₂, …, C_n из некоторой области n-мерного пространства) является частным решением уравнения ; 2. Любое частное решение уравнения может быть получено из общего решения при некотором наборе постоянных C₁, C₂, …, C_n. Основную теорему - теорему о существовании и единственности решения задачи Коши для уравнения n-го порядка -мы сформулируем для записи уравнения в форме, разрешённой относительно старшей производной: . 14.4.1. Постановка задачи Коши для уравнения n-го порядка: требуется найти решение уравнения

;

(17)

удовлетворяющее начальным условиям

(18)

где y₀, y₁, y₂, …, y_n-1 - заданные числа. В случае уравнения второго порядка это означает, что требуется найти решение, проходящее через заданную точку (x₀, y₀,) с заданным угловым коэффициентом y₁.

14.4.2.1. Уравнение вида решается последовательным n-кратным интегрированием. Пример: Переобозначив постояные, общее решение запишем в виде y = cos x + C₁x³ + C₂x² + C₃x + C₄. 14.4.2.2. Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x, y^(k), y^(k+1), y^(k+2), …,y⁽ⁿ⁾) = 0, не содержащего функции y(x) и k - 1 младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y^(k)(x). Тогда z^(n-k) = y⁽ⁿ⁾(x), и относительно z(x) уравнение примет вид , т.е. будет уравнением n - k-го порядка. После нахождения z(x) последовательным интегрированием решается уравнение y^(k) = z(x). Пример: решить задачу Коши: . Младшая производная, входящая в явной форме в уравнения, - вторая, поэтому делаем замену искомой функции . Тогда , и уравнение примет вид . Это - уравнение Бернулли; пусть z = uv, тогда , , , 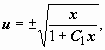следовательно, 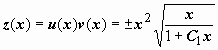. Относительно y(x) - это уравнение . Мы можем последовательно находить и так далее, однако в этом нет необходимости. Так как мы решаем задачу Коши, то из начального условия при x = 1 можно определить и знак частного решения, и значение постоянной C₁: 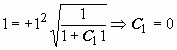. Теперь 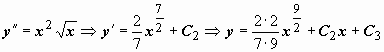. Из условия при x = 1 находим C₂: 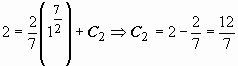; из условия y = 3 при x = 1 находим C₃: 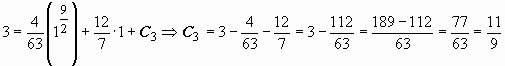. Окончательный ответ: . 14.4.2.3. Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения , не содержащего явно x, может быть понижен на 1 с помощью красивого искусственного приёма, который заключается в том, что вводится новая функциональная зависимость от y: . Старшие производные y по x вычисляются по правилу дифференцирования сложной функции: .

Аналогично, Также находятся следующие производные, и всегда k -ая производная y по x выражается через k-1 -ую производную p по y. В случае уравнения второго порядка в результате таких преобразований получим , т.е. уравнение первого порядка (в котором y выступает как аргумент, p(y) - как неизвестная функция). После нахождения решения p = p(y, C₁) этого уравнения решается уравнение , решение которого y = y(x, C₁, C₂) будет общим решением исходного уравнения. Примеры: 1. Задача Коши . Переменная x явно в уравнение не входит, поэтому полагаем , , тогда . Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений , поэтому рассматриваем два случая: 1. ; 2. Это - уравнение с разделяющимися переменными: . Получено уравнение , решаем его: . Это общее решение уравнения, в данном случае оно включает в себя решение y = C при C₂ = 0. Находим значения постоянных, при которых удовлетворяются начальные условия: из . Далее, из следует, что , т.е. C₂ = 0. Частное решение - , т.е. y = 2. Пример 2. Решение: 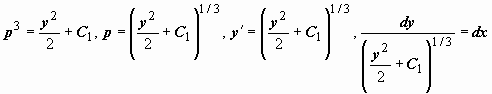. Интеграл от дифференциала в левой части этого равенства вообще не берётся, поэтому проверим, не упростится ли задача, если использовать начальные условия. Так как при x = 0 должно быть , то получим 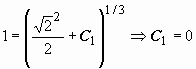. Поэтому частное решение должно удовлетворять уравнению 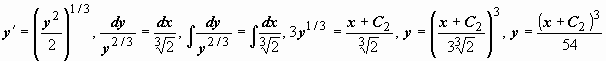. Находим : . Ответ: решение задачи Коши .

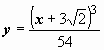14.4.2.4. Применение интегрируемых комбинаций. Иногда удаётся заметить, что в уравнении правая часть является производной некоторой функции , т.е. уравнение имеет вид . Интегрируя по x, получим уравнение, порядок которого на единицу меньше порядка исходного уравнения (так называемый первый интеграл уравнения): . Пример: . Если переписать это уравнение в виде 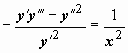и сообразить, что справа стоит производная функции , то получим , откуда . Это уравнение не содержит явно y, поэтому .

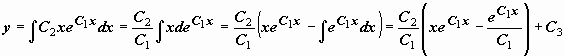1. Если y₁(x) и y₂(x)— два решения линейного однородного дифференциального уравнения

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0

то любая их линейная комбинация y(x) = C₁y₁(x) + C₂y₂(x) является решением этого однородного уравнения.

2. Если y₁(x) и y₂(x) — два решения линейного неоднородного уравнения L(y) = f(x) , то их разность y(x) = y₁(x) − y₂ (x) является решением однородного уравнения L(y) = 0 .

 

3. Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма любого фиксированного (частного) решения неоднородного уравнения и некоторого решения однородного уравнения.

 

4. Если y₁(x) и y₂(x) — решения линейных неоднородных уравнений L(y) = f₁(x) и L(y) = f₂(x) соответственно, то их сумма y(x) = y₁(x) + y₂(x) является решением неоднородного уравнения L(y) = f₁(x) + f₂(x).

 

Обычно именно это последнее утверждение называют принципом суперпозиции.

Необходимое условие линейной зависимости функций.

Справедливо следующее необходимое условие линейной зависимости функций: если функции y₁(x), y₂(x), ..., y_n(x), линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно обращается в нуль на этом отрезке: W(x; y₁(x), y₂(x), ..., y_n(x)) ≡ 0. 

Однако, если определитель Вронского функций отличен от нуля хотя бы в одной точке отрезка [a; b] , то функции линейно независимы.

 

Это последнее утверждение — достаточное условие линейной независимости функций.

Теорема 1 Если n функций 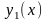, , …, линейно зависимы на промежутке , то вронскиан этих функций , .

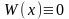Доказательство: Из определения линейной зависимости следует, что существуют числа 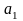, , …, , 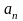среди которых не все равны нулю, такие, что

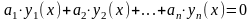
тождественно относительно переменной 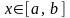. Дифференцируя это равенство 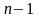раз, получим

.

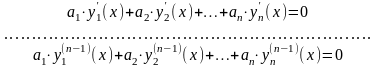Эти n равенств образуют систему n линейных однородных уравнений с n неизвестными , , …, , которая имеет по условию ненулевое решение. Поэтому определитель системы должен быть равен нулю, т.е. 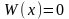при любом .

Теорема 2 Если определитель Вронского n функций , , …, не равен тождественно нулю на промежутке , то эти функции линейно независимы.

Доказательство теоремы 2 вытекает из теоремы 1 при предположении противного.

Теоремы, обратные теоремам 1 и 2 неверны: линейно независимые функции на некотором промежутке могут иметь определитель Вронского, тождественно равный нулю на этом промежутке.

Теорема. Если решения , , …, ЛОДУ порядка n

,

(6.29)

линейно независимы на промежутке , то их определитель Вронского не обращается в нуль ни в одной точке этого промежутка.

Доказательство. В теореме предполагается, что коэффициенты дифференциального оператора 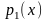, , 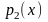…, непрерывны на промежутке и, следовательно, теорема существования и единственности имеет место для уравнения (п.6.5.1).

По условию функции , , …, являются решениями уравнения , и по свойству 3 (п. 6.5.2) линейного оператора L любая линейная комбинация этих функций удовлетворяет уравнению , т.е. функция

,

(6.30)

удовлетворяет уравнению при любых постоянных , …, 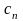. Пусть – произвольная точка. Найдём частное решение уравнения (6.29), удовлетворяющее нулевым начальным условиям

, , …, .

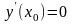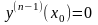Согласно замечанию к теореме существования и единственности ЛОДУ (п. 6.5.1) имеется одно и только одно решение 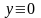(тривиальное решение). Из линейной комбинации (6.30) оно получается при , , …, , 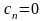так как функции , , …, линейно независимы. Это же тривиальное решение можно получить, отыскивая коэффициенты , …, , подставляя 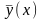в начальные условия. При этом получаем систему уравнений относительно , …, :

Определителем этой системы является вронскиан 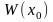. Из предыдущего следует, что эта система имеет единственное решение , , …, , и, следовательно, . Точка есть произвольная точка промежутка , поэтому в любой точке . Теорема доказана.
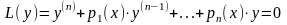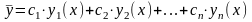