Уравнения первого порядка, не разрешенные относительно производной
1°. Уравнение, содержащее только :
Это
уравнение имеет общий интеграл
П.
11.1
Общий
интеграл уравнения
П.
11.2
Общий
интеграл уравнения
2°. Уравнение, не содержащее искомой функции:
(11.1)
Рассмотрим два случая.
1.
Уравнение (11.1)
разрешимо относительно
Пусть оно определяет m значений :
.
Тогда, интегрируя, получаем:
П.
11.3
Интегрируя,
получаем два
семейства кривых:
2. Уравнение (11.1) не разрешимо (в элементарных функциях) относи-тельно но допускает параметрическое представление:
Так
как
то
Интегрируя, найдем:
Таким
образом, получаем общее решение в
параметрической форме:
П.
11.4
Полагаем
тогда
Далее,
Т.
о., общее решение
П.
11.5
Вначале
сделаем замену
Так
как
Поэтому
(ввели под
знак
дифференциала t2
и сделали замену z=t3
).
Преобразуем дробь
.
,
Т.
о., общее решение
3°. Уравнение, не содержащее независимой переменной:
(11.2)
Рассмотрим два случая.
1.
Уравнение (11.2)
разрешимо относительно
Тогда
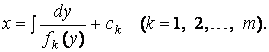
П.
11.6
Разрешаем
уравнение относительно
Интегрируя,
находим общее решение
и
2. Уравнение (11.2) не разрешимо (в элементарных функциях) относи-тельо но допускает параметрическое представление:
Тогда
Общее решение в параметрической форме:
П.
11.7
Полагаем
Тогда
Общее
решение в па-раметрической форме:
3°. Уравнение Лагранжа:
Положим
тогда
Считаем, что
Поэтому
или
1).
тогда
Получили линейное уравнение. Пусть его
решение
Тогда общее решение можно записать в
пара-метрической форме:
2).
пусть
корни этого уравнения, тогда получаем:
.
Эти прямые линии могут оказаться
осо-быми решениями уравнения Лагранжа.
П.
11.8
Делаем
замену
тогда
Делаем
замену
Таким
образом, общее решение в пара-метрической
форме:
