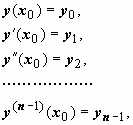- •Часть 1
- •[Править] Интегрирующий множитель
- •[Править] Алгоритм решения
- •2. Уравнение не разрешимое относительно производной.
- •Уравнения, не разрешимые относительно производной
- •Пусть уравнение можно разрешить относительно т.Е. Записать в виде Введя параметр (7.1)
- •Уравнения Лагранжа и Клеро
- •Задания для работы на семинаре
- •Задания для самостоятельной работы
- •Уравнения высших порядков.
- •4. Линейные уравнения высших порядков.
- •Часть II
- •1. Дифференциальные уравнения с разделяющимися переменными.
- •Первый способ
- •[Править] Второй способ
- •[Править] Интегрирующий множитель
- •[Править] Алгоритм решения
- •Уравнения первого порядка, не разрешенные относительно производной
- •1°. Уравнение, содержащее только :
- •2°. Уравнение, не содержащее искомой функции:
- •3°. Уравнение, не содержащее независимой переменной:
- •3°. Уравнение Лагранжа:
- •4°. Уравнение Клеро:
- •6.5.5 Фундаментальная система решения лоду порядка n
- •6.5.6 Структура общего решения лоду порядка n
- •6.5.7 Частный случай лоду второго порядка. Формула Лиувилля-Остроградского
- •6.5.8 Линейные неоднородные дифференциальные уравнения. Структура общего решения. Метод вариации произвольных постоянных
- •6.6 Линейные дифференциальные уравнения порядка n с постоянными коэффициентами
- •6.6.1 Нахождение общего решения линейного однородного уравнения порядка n с постоянными коэффициентами
- •6.6.2 Нахождение общего решения линейного неоднородного уравнения порядка n с постоянными коэффициентами со специальной правой частью
- •7.1.Метод вариации произвольных постоянных (метод Лагранжа) решения лнду.
Пусть уравнение можно разрешить относительно т.Е. Записать в виде Введя параметр (7.1)
получим  (7.2)
(7.2)
Взяв
полный дифференциал от обеих частей
равенства (7.2) и заменив
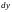 на
на
 (из
(7.1)), получим уравнение вида
(из
(7.1)), получим уравнение вида 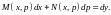
Если
решение этого уравнения найдено в виде
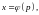 то воспользовавшись равенством (7.2),
получим решение исходного уравнения в
параметрической записи:
то воспользовавшись равенством (7.2),
получим решение исходного уравнения в
параметрической записи:

Замечание.
Уравнение
вида
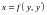 решаются тем же методом.
решаются тем же методом.
Пример
7.2. Решить
уравнение
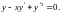
Данное
уравнение разрешимо относительно
 :
:
 (7.3)
(7.3)
Полагая
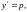 выражение
(7.3) перепишется в виде
выражение
(7.3) перепишется в виде
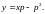 (7.4)
(7.4)
Продифференцируем
обе части равенства (7.4), приняв во
внимание, что
 Получим
Получим

Последнее
уравнение дает решения
 Подставляя полученные решения в (7.4)
получаем решения исходного уравнения:
Подставляя полученные решения в (7.4)
получаем решения исходного уравнения:
а)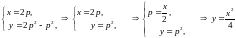
б)

Общее
решение 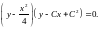
Пример
7.3. Решить
уравнение

Данное
уравнение разрешимо относительно x:
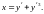
Полагая
получаем
 Продифференцировав обе части последнего
выражения и заменяя
Продифференцировав обе части последнего
выражения и заменяя
 на
на
 получаем
получаем
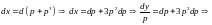
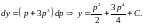
Таким
образом, имеем общее решение в
параметрической форме 
Уравнения Лагранжа и Клеро
Уравнение
Лагранжа
имеет вид
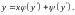 Полагая
дифференцируя по
Полагая
дифференцируя по
 и
заменяя
на
и
заменяя
на
 приводим это уравнение к линейному
относительно
как функцию
приводим это уравнение к линейному
относительно
как функцию
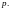 Находя решение этого последнего уравнения
Находя решение этого последнего уравнения
 получаем общее решение исходного
уравнения в параметрической форме:
получаем общее решение исходного
уравнения в параметрической форме: 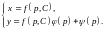
Пример
7.4.
Решить
уравнение
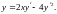
Данное
уравнение является уравнением Лагранжа,
т.к. 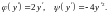
Введение
параметра
 с последующим дифференцированием обеих
частей уравнения приводит к следующему
соотношению:
с последующим дифференцированием обеих
частей уравнения приводит к следующему
соотношению:
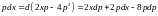 или
или
 или
или
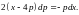
Используя
замену,
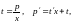 сводим последнее выражение к уравнению
в разделяющихся переменных
сводим последнее выражение к уравнению
в разделяющихся переменных
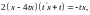
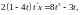
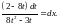
Интегрируя
последнее выражение, получим
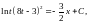
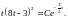
Подставляя
обратную замену
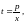 получим общее решение исходного уравнения
получим общее решение исходного уравнения
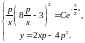
Уравнение
Клеро
имеет вид
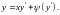 Метод решения тот же, что и для уравнения
Лагранжа. Общее решение уравнения Клеро
имеет вид
Метод решения тот же, что и для уравнения
Лагранжа. Общее решение уравнения Клеро
имеет вид
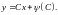
Пример
7.5.
Решить уравнение
 Исходное
уравнение является уравнением Клеро.
Введем параметр
Исходное
уравнение является уравнением Клеро.
Введем параметр
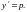
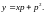 (7.5)
(7.5)
Продифференцируем
обе части уравнения (7.5), получим 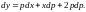
Заменяя
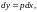 получим
получим
 Решая последнее уравнение, получим
Решая последнее уравнение, получим
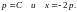 Подставляя
их в (7.5), получим общее решение данного
уравнения
Подставляя
их в (7.5), получим общее решение данного
уравнения
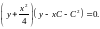
Задания для работы на семинаре
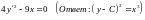 .
.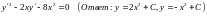 .
.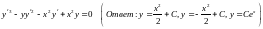 .
.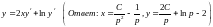 .
.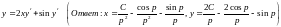 .
.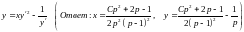 .
. .
.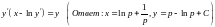 .
.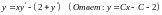 .
. .
.
Задания для самостоятельной работы
 .
.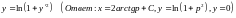 .
.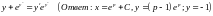 .
.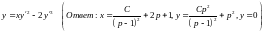 .
.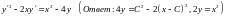 .
. .
. .
.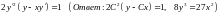 .
.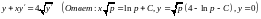 .
.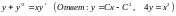 .
.
Уравнения высших порядков.
Опр. Общим решением (общим интегралом) уравнения называется такое соотношение
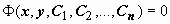 ,
что:
,
что:
 1.
Любое решение
1.
Любое решение
 этого
соотношения относительно y
(для набора постоянных C1,
C2,
…, Cn
из некоторой области n-мерного
пространства) является частным решением
уравнения ;
2.
Любое частное решение уравнения может
быть получено из общего решения
при
некотором наборе постоянных C1,
C2,
…, Cn.
Основную
теорему - теорему о существовании и
единственности решения задачи Коши
для уравнения n-го
порядка -мы сформулируем для записи
уравнения в форме, разрешённой
относительно старшей производной:
этого
соотношения относительно y
(для набора постоянных C1,
C2,
…, Cn
из некоторой области n-мерного
пространства) является частным решением
уравнения ;
2.
Любое частное решение уравнения может
быть получено из общего решения
при
некотором наборе постоянных C1,
C2,
…, Cn.
Основную
теорему - теорему о существовании и
единственности решения задачи Коши
для уравнения n-го
порядка -мы сформулируем для записи
уравнения в форме, разрешённой
относительно старшей производной:
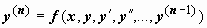 .
14.4.1.
Постановка задачи Коши для уравнения
n-го
порядка:
требуется найти решение уравнения
.
14.4.1.
Постановка задачи Коши для уравнения
n-го
порядка:
требуется найти решение уравнения
;
(17)
удовлетворяющее начальным условиям
|
Теорема
существования и единственности решения
задачи Коши: Пусть функция f(x,
y, p1,
p2,
…, pn-1)
непрерывна и имеет непрерывные частные
производные
![]() в
некоторой области D n +
1-мерного евклидового пространства
переменных (x, y, p1,
p2,
…, pn-1),
и пусть точка (x0,
y0,
y1,
y2,
…, yn-1)
принадлежит области D. Тогда в
некоторой окрестности точки x0
существует решение уравнения (17),
удовлетворяющее начальным условиям
(18). Это решение единственно.
в
некоторой области D n +
1-мерного евклидового пространства
переменных (x, y, p1,
p2,
…, pn-1),
и пусть точка (x0,
y0,
y1,
y2,
…, yn-1)
принадлежит области D. Тогда в
некоторой окрестности точки x0
существует решение уравнения (17),
удовлетворяющее начальным условиям
(18). Это решение единственно.
Уравнение
вида
![]() решается
последовательным n-кратным
интегрированием. Пример:
решается
последовательным n-кратным
интегрированием. Пример:
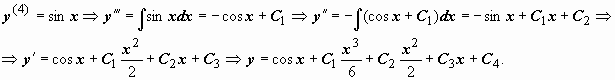 Переобозначив
постояные, общее решение запишем в виде
y = cos x + C1x3
+ C2x2 + C3x
+ C4.
Переобозначив
постояные, общее решение запишем в виде
y = cos x + C1x3
+ C2x2 + C3x
+ C4.
Уравнение,
не содержащее в явном виде неизвестную
функцию и её младшие производные.
Порядок уравнения вида F(x,
y(k),
y(k+1),
y(k+2),
…,y(n))
= 0, не содержащего функции y(x)
и k - 1 младшую производную этой
функции в явном виде, может быть понижен
ровно на k единиц введением новой
неизвестной функции z(x)
= y(k)(x).
Тогда
![]() z(n-k)
= y(n)(x),
и относительно z(x)
уравнение примет вид
z(n-k)
= y(n)(x),
и относительно z(x)
уравнение примет вид
![]() ,
т.е. будет уравнением n - k-го
порядка. После нахождения z(x)
последовательным интегрированием
решается уравнение y(k)
= z(x).
,
т.е. будет уравнением n - k-го
порядка. После нахождения z(x)
последовательным интегрированием
решается уравнение y(k)
= z(x).
Уравнение,
не содержащее в явном виде независимую
переменную x.
Порядок
уравнения
![]() ,
не содержащего явно x,
может быть понижен на 1 с помощью красивого
искусственного приёма, который заключается
в том, что вводится новая функциональная
зависимость
,
не содержащего явно x,
может быть понижен на 1 с помощью красивого
искусственного приёма, который заключается
в том, что вводится новая функциональная
зависимость
![]() от
y:
от
y:
![]() .
Старшие производные y
по x
вычисляются
по правилу дифференцирования сложной
функции:
.
Старшие производные y
по x
вычисляются
по правилу дифференцирования сложной
функции:
![]() .
.
Аналогично,
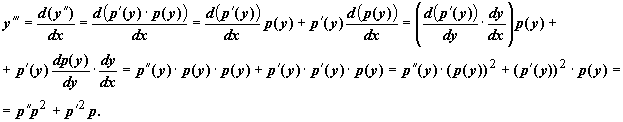 Также
находятся следующие производные, и
всегда k
-ая производная y
по x
выражается через k-1
-ую производную p
по
y.
В случае уравнения второго порядка
Также
находятся следующие производные, и
всегда k
-ая производная y
по x
выражается через k-1
-ую производную p
по
y.
В случае уравнения второго порядка
![]() в
результате таких преобразований получим
в
результате таких преобразований получим
![]() ,
т.е. уравнение первого порядка (в котором
y
выступает как аргумент, p(y)
- как неизвестная функция). После
нахождения решения p
= p(y,
C1)
этого уравнения решается уравнение
,
т.е. уравнение первого порядка (в котором
y
выступает как аргумент, p(y)
- как неизвестная функция). После
нахождения решения p
= p(y,
C1)
этого уравнения решается уравнение
![]() ,
решение которого y
= y(x,
C1,
C2)
будет общим решением исходного уравнения.
,
решение которого y
= y(x,
C1,
C2)
будет общим решением исходного уравнения.