[Править] Интегрирующий множитель

Непрерывная функция в называется интегрирующим множителем уравнения (1), если уравнение является уравнением в полных дифференциалах, то есть для некоторой функции . Число интегрирующих множителей данного уравнения бесконечно.

Функция является интегрирующим множителем уравнения (1) тогда и только тогда, когда она удовлетворяет уравнению

(область по-прежнему полагаем односвязной; уравнение (2) является следствием признака уравнения в полных дифференциалах).

Уравнение (2) в общем виде решается сложнее, чем (1), но для интегрирования (1) достаточно знать один интегрирующий множитель, то есть найти какое-либо одно решение уравнения (2). Обычно ищут решение (2) в виде или , но это не всегда возможно.

[Править] Алгоритм решения

(1)

(2)

(3)

Возьмём (3).1 и проинтегрируем по переменной t:

(*)

Подставим в (3).2:

В получившемся равенстве слагаемые, содержащие t, уничтожатся. Получим: . Проинтегрируем по x и подставим в (*).

Всегда можно привести его к уравнению такого типа умножением на некоторую не равную нулю функцию , называемую интегрирующим множителем. Но не всегда легко найти такую функцию.

Если интегрирующий множитель уравнения (1), уравнение

является уравнением в полных дифференциалах:

,

т.е. интегрирующий множитель есть решение уравнения

                                                      .                                                        (5)

Найти функцию из уравнения (5) в общем случае довольно сложно. В частных случаях соотношение (5) значительно упрощается.

Случай 1. Если уравнение (1) имеет интегрирующий множитель, зависящий только от x, т.е. , то из (5) имеем

.

Случай 2. Если уравнение (1) допускает интегрирующий множитель как функцию одной переменной y, т.е. , то

.

Случай 3. Если уравнение (1) имеет интегрирующий множитель вида , где - известная функция, то

.

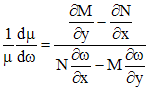Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.

2. Уравнение не разрешимое относительно производной.

Уравнение (11.2) не разрешимо (в элементарных функциях) относи-тельо но допускает параметрическое представление:

Тогда

Общее решение в параметрической форме:

http://www.nsc.ru/rus/textbooks/akhmerov/ode_unicode/s-06/s-06.html

Уравнения, не разрешимые относительно производной

1. Уравнения вида можно решать следующими методами:

а) разрешить уравнение относительно , т.е. из уравнения выразить через Получится одно или несколько уравнений вида Каждое из них надо решить.

Пример 7.1 Решить уравнение Решая данное квадратное уравнение относительно производной, получаем два дифференциальных уравнения первого порядка:

Оба уравнения являются уравнениями с разделяющимися переменными, поэтому их общими решениями являются

Общий интеграл исходного уравнения можно записать в виде

б) метод введения параметра.