Часть 1

1 Уравнения первого порядка интегрируемые в квадратурах.

Опр:

Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,y⁽ⁿ⁾(x) до порядка n включительно и удовлетворяющая этому уравнению.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Общее решение дифференциального уравнения — функция наиболее общего вида, которая при подстановке в дифференциальное уравнение вида

обращает его в тождество.

Частным решением дифференциального уравнения на интервале называется каждая функция y(x), которая при подстановке в уравнение вида

обращает его в верное тождество на интервале .

Осо́бое решен́ие обыкновенного дифференциального уравнения — решение, в любой окрестности каждой точки которого нарушается единственность решения задачи Коши для этого уравнения.

Рассмотрим уравнение

F(x,y,y') = 0, (1) где F(x,y,p) — заданная непрерывная функция в некоторой области .

Решение уравнения (1) , называется особым решением, если каждая точка , его интегральной кривой является точкой локальной неединственности решения задачи Коши.

Особое решение , уравнения (1) геометрически означает, что интегральная кривая для y = ψ(x) в каждой своей точке касается некоторой другой интегральной кривой уравнения (1) и не совпадает с ней в некоторой окрестности этой точки.

Пусть Φ(x,y,C) является общим решением дифференциального уравнения F(x,y,y') = 0. Графически уравнение Φ(x,y,C) = 0 соответствует семейству интегральных кривых на плоскости xy. Если функция Φ(x,y,C) и ее частные производные непрерывны, то огибающая семейства интегральных кривых общего решения определяется системой уравнений:

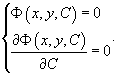
Теорема Коши. Пусть в области D из Rⁿ⁺¹ непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y:

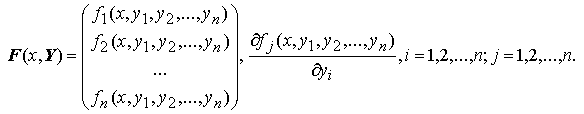
Тогда, какова бы ни была начальная точка (x₀,Y₀) ≡ (x₀,y_{1, 0} ,y_{2, 0}, … ,y_{n, 0} ) ∈ D , существует такой отрезок [x₀ − h; x₀ + h] , что задача Коши   Y' = F(x,Y), что Y(x₀)=Y₀ имеет единственное решение.

Важно понимать, что теорема Коши имеет локальный характер: существование решения Y = Y(x) гарантируется лишь в достаточно малой окрестности точки x₀ , ( h > 0 может оказаться достаточно малым).

Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения — при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.

Типы:

Дифференциальное уравнение

(3.1)

называется уравнением с разделяющимися переменными.

Умножая обе части уравнения на , получаем уравнение

(3.2)

В уравнении (3.2) коэффициент при dx зависит только от x, а коэффициент при dy зависит только от y. Значит, в уравнении (3.2) переменные разделены. Интегрируя, получаем:

∫ +∫

Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид

   (7)

Подстановка ; ; , где  преобразует это уравнение к уравнению с разделяющимися переменными.

  ,   ,  .

Замечание. Функция  называется однородной степени , если , где  - некоторая константа. Например, функция   является однородной функцией степени два.

Дифференциальное уравнение называется квазиоднородным, если для любого выполняется соотношение . Данное уравнение решается заменой :

В силу квазиоднородности, положив , получаем:

, что, очевидно, является однородным уравнением.

Дифференциальные уравнения вида   называются линейными.

Метод Бернулли Решение уравнения   ищется в виде  . При этой замене получаем:  . Функцию  выбирают из условия  . Полученную функцию   подставляют в уравнение  (учитываем  ), решая которое находят функцию  .

   Уравнение Бернулли

Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

где a(x) и b(x) − непрерывные функции. Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда m = 1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z(x) имеет вид

Если в уравнении (1) левая часть представляет собой полный дифференциал, то есть , то такое уравнение называется уравнением в полных дифференциалах (частный случай так называемого пфаффова уравнения). Интегральные кривые такого уравнения суть линии уровней функции , т.е. определяются уравнением при всевозможных значениях произвольной постоянной .

Если в области выполнено условие , то общее решение уравнения (1) определяется из уравнения как неявная функция . Через каждую точку области проходит единственная интегральная кривая уравнения (1).

Если рассматриваемая область односвязна, а производные также непрерывны в , то для того, чтобы (1) было уравнением в полных дифференциалах, необходимо и достаточно выполнения условия

(признак уравнения в полных дифференциалах).