25 Инерционно-форсирующее звено

Инерционно-форсирующее звено называют также интегро-дифференцирующим или упругим звеном, описывается оно дифференциальным уравнением первого порядка

Ty'(t) + y(t) = k[T₀x'(t) + x(t)]. (3.50)

Существенным параметром звена является коэффициент Если τ < 1, то звено по своим свойствам приближается к интегрирующему и инерционному звеньям, если же τ > 1, то звено ближе к дифференцирующим звеньям. Передаточная функция звена:

(3.51)

Частотные характеристики получают в результате замены s = iω:

АФХ (3.52)

АЧХ (3.53)

ФЧХ (3.54)

Графики частотных характеристик для τ > 1 и τ < 1 изображены соответственно на рис. 3.15 и 3.16.

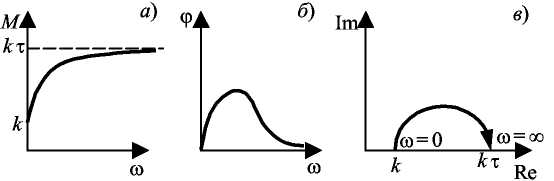
Рис. 3.15 Частотные характеристики инерционно-форсирующего звена для τ > 1:

а - АЧХ; б - ФЧХ; в - АФХ

Рис. 3.16 Частотные характеристики инерционно-форсирующего звена для τ < 1:

а -АЧХ;б-ФЧХ;в-АФХ

Используя взаимосвязь динамических характеристик, записываются уравнения переходной и весовой функций, соответственно

(3.55)

(3.56)

их графики для τ > 1 и τ < 1 изображены на рис. 3.17. и 3.18.

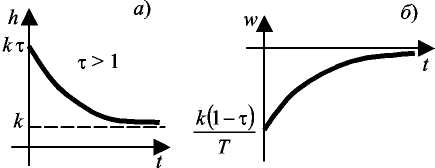
Рис. 3.17 Переходные характеристики инерционно-форсирующего звена для τ> 1:

а - переходная функция; б - весовая функция

Рис. 3.18 Переходные характеристики инерционно-форсирующего звена для τ< 1:

а — переходная функция; б — весовая функция

24 Апериодическое звено второго порядка

Уравнение апериодического звена второго порядка удобно записать в виде

T₁T₂y''(t) + (T₁ + T₂)y′(t) + y(t) = kx(t), (3.57)

где T₁, T₂ — постоянные времени; k— коэффициент усиления; T₁, T₂, k> 0. После преобразования (3.57) по Лапласу

[T₁T₂s² + (T₁ + T₂)s + 1]y(s) = kx(s),

откуда передаточная функция звена равна:

(3.58)

Апериодическое звено второго порядка можно структурно представить в виде последовательного соединения двух звеньев первого порядка с постоянными времени Т₁ и T₂ (рис. 3.19), поэтому оно не относится к числу элементарных. Корни характеристического уравнения действительные.

Частотные характеристики, графики которых изображены на рис. 3.20:

АФХ (3.59)

АЧХ (3.60)

ФЧХ (3.61)

Рис. 3.19 Структурная схема апериодического звена второго порядка

Рис. 3.20 Частотные характеристики апериодического звена второго порядка:

а - АЧХ; б - ФЧХ; в - АФХ

Для сравнения пунктиром показаны характеристики звена первого порядка. Амплитудно-частотная характеристика при изменении частоты от 0 до ∞ изменяется от k до 0. Фазочастотная характеристика изменяется от 0 до -π. Годограф амплитудно-фазовой характеристики лежит в 4-м и 3-м квадрантах. Сравнивая частотные характеристики звена первого порядка, видно, что добавление второго звена первого порядка увеличивает инерционность объекта, увеличивает модуль и увеличивает отставание по фазе.

Уравнение переходной функции в операторной форме имеет вид

Переходя к оригиналу, получают

(3.62)

Переходная функция представляет собой неколебательную кривую, имеющую одну точку перегиба и асимптотически стремящуюся кy(∞) = k. Уравнение весовой функции:

(3.63)

Графики переходных характеристик изображены на рис. 3.21.

Рис. 3.21 Переходные характеристики апериодического звена второго порядка:

а — переходная функция; б — весовая функция