
- •Изоморфизм
- •Матричное задание графа
- •Свойства матрицы смежности
- •Операции над графами
- •Достижимость и связность
- •Матрицы достижимости и контрдостижимости
- •Нахождение сильных компонент
- •Конденсация графа
- •Базы и антибазы
- •Построение компонент связности в неориентированном графе
- •Построение компонент связности в ориентированном графе
- •Система независимых циклов
- •Дерево. Остов граф
- •Процесс восстановления дерева по набору
- •Алгоритм построения произвольного остова
- •Определение минимального остова
- •Алгоритм построения системы независимых циклов графа
- •Модификация Форда
- •Алгоритмы поиска всех кратчайших путей
- •Алгоритм Флойда
- •Алгоритм Флойда
- •Алгоритм Данцига
- •Алгоритм Данцига
- •Раскраска
- •Метод построения функции Гранди на графе
- •Гамильтоновы пути, контуры и задача Коммивояжера
- •Метод Роберта и Флореса (перебор-метод для орграфов)
- •Алгоритм поиска увеличивающего пути
- •Алгоритм поиска максимального потока
- •Алгоритм Форда и Фалкерсона
- •Модификация алгоритма поиска максимального потока при нескольких источниках и стоках
- •Алгоритм поиска потока минимальной стоимости
- •Алгоритм поиска потока минимальной стоимости
- •Алгоритмы построения покрывающих деревьев
Алгоритм Флойда
Определить матрицу , задав величину каждого её элемента (i,j), равную длине кратчайшего пути, соединяющего вершину i с вершиной j.
Если в указанном
графе вершины не соединены дугами,
то полагается
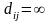 ,
а все
,
а все
диагональные элементы равны 0.
Для целого m, последовательно принимающего значения 1, 2, ..., n, определить по величинам элементов матрицы величины элементов матрицы , исследуя соотношения (2).
При увеличении каждого элемента матрицы фиксировать соответствующий путь.
Замечание:
Поскольку
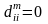 ,
то нет необходимости в вычислении
диагональных элементов матриц
,
то нет необходимости в вычислении
диагональных элементов матриц
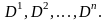
Кроме того, для
всех i
= 1, 2, ..., n
имеет место соотношения
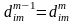 и
и
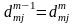 .
Следовательно, при определении матрицы
нет необходимости в пересчёте элементов
m-
ой строки и m-
ого столбца матрицы
.
.
Следовательно, при определении матрицы
нет необходимости в пересчёте элементов
m-
ой строки и m-
ого столбца матрицы
.
Алгоритм Данцига
Вершины исходного графа перенумеруем целыми числами от 1 до n и обозначим через длину кратчайшего пути из вершины i в вершину j, в котором допускается использование в качестве промежуточных m первых вершин графа.
Матрица
,
состоящая из элементов
при
каждом
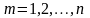 имеет размерность не
,
а
имеет размерность не
,
а
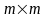 .
.
Требуется
определить матрицу
,
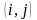 -ый
элемент которой определяет длину
кратчайшего пути из вершины i
в вершину j.
-ый
элемент которой определяет длину
кратчайшего пути из вершины i
в вершину j.
В этом алгоритме
матрица
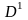 определяется из матрицы
,
определяется из матрицы
,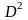 из
,
из
из
,
из
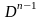 .
.
Каждая новая вычисляемая матрица содержит на 1 строку и 1 столбец больше, чем ее предшественница .
Элементы матрицы
,
не входящие в последнюю строку и в
последний столбец, число которых
(элементов), равное
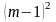 ,
определяется также как и в методе
Флойда.
,
определяется также как и в методе
Флойда.
Элементы последней
строки и последнего столбца матрицы
вычисляются с учетом следующих
соображений: кратчайший путь из i
в m,
в котором допускается использование
в качестве промежуточных только n-первых
вершин графа, должен иметь своей первой
частью
кратчайший путь из вершины i
в некоторую вершину j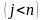 ,
который
допускает использование в качестве
промежуточных только n
- первых вершин графа, а второй
частью –
кратчайшую дугу, ведущую из вершины j
в вершину m.
,
который
допускает использование в качестве
промежуточных только n
- первых вершин графа, а второй
частью –
кратчайшую дугу, ведущую из вершины j
в вершину m.
Аналогично,
кратчайший путь из вершины m
в вершину i
, в котором допускается использование
в качестве промежуточных только m-первых
вершин графа, должен иметь своей первой
частью -
кратчайшую дугу, ведущую из вершины m
в некоторую вершину j
 ,
а второй
частью –
кратчайший путь из вершины j
в вершину i,
который допускает использование в
качестве промежуточных только
,
а второй
частью –
кратчайший путь из вершины j
в вершину i,
который допускает использование в
качестве промежуточных только
 - первых вершин графа (следует рассматривать
только такие вершины j,
для которых имеется хотя бы одна дуга,
ведущая из вершины m
в вершину j).
- первых вершин графа (следует рассматривать
только такие вершины j,
для которых имеется хотя бы одна дуга,
ведущая из вершины m
в вершину j).
Все величины
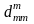 должны полагаться равными 0.
должны полагаться равными 0.
Алгоритм Данцига
Сформировать матрицу размером , элемент которой определяет длину кратчайшей дуги, ведущей из вершины i в вершину j (если такой дуги нет, то полагаем
 ).
).Последовательно определить элементы матрицы из элементов матрицы
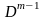 для
для
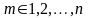 согласно формулам:
согласно формулам:
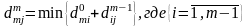 (1)
(1)
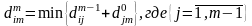 (2)
(2)
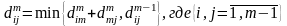 (3)
(3)
