
- •Изоморфизм
- •Матричное задание графа
- •Свойства матрицы смежности
- •Операции над графами
- •Достижимость и связность
- •Матрицы достижимости и контрдостижимости
- •Нахождение сильных компонент
- •Конденсация графа
- •Базы и антибазы
- •Построение компонент связности в неориентированном графе
- •Построение компонент связности в ориентированном графе
- •Система независимых циклов
- •Дерево. Остов граф
- •Процесс восстановления дерева по набору
- •Алгоритм построения произвольного остова
- •Определение минимального остова
- •Алгоритм построения системы независимых циклов графа
- •Модификация Форда
- •Алгоритмы поиска всех кратчайших путей
- •Алгоритм Флойда
- •Алгоритм Флойда
- •Алгоритм Данцига
- •Алгоритм Данцига
- •Раскраска
- •Метод построения функции Гранди на графе
- •Гамильтоновы пути, контуры и задача Коммивояжера
- •Метод Роберта и Флореса (перебор-метод для орграфов)
- •Алгоритм поиска увеличивающего пути
- •Алгоритм поиска максимального потока
- •Алгоритм Форда и Фалкерсона
- •Модификация алгоритма поиска максимального потока при нескольких источниках и стоках
- •Алгоритм поиска потока минимальной стоимости
- •Алгоритм поиска потока минимальной стоимости
- •Алгоритмы построения покрывающих деревьев
Алгоритм построения произвольного остова
Для каждой компоненты i графа выполняются пункты 2 и 3.
Строим частичный граф, содержащий все Ni вершины компоненты и не содержащий ребер (нуль-граф) (Ni -1)
Если в текущий граф уже включены (Ni -1) ребер, то остов для i-ой компоненты построен, иначе выбираем очередное нерассмотренное ребро компоненты и пытаемся включить его в граф. Если в текущем графе включаемое ребро не приводит к образованию цикла, то включаем это ребро, иначе не включаем. Ребро считается при этом рассмотренным. Повторяем шаг 3.
Определение минимального остова
Для взвешенного графа остов с минимальной суммой весов вошедших в него ребер
называется минимальным (кратчайшее связывающее дерево). Аналогию можно провести и в случае обозначения длины ребер.
Алгоритм построения системы независимых циклов графа
Строится произвольный остов графа, а в исходном графе отмечаются ребра, включенные в остов.
Выбираем очередное неотмеченное ребро и строим цикл, включающий это ребро и ребра остова. Он обязательно существует, так как вершины остова связны. Рассмотренное ребро отмечается и, если есть еще неотмеченные ребра, то выполняется шаг 2, иначе - шаг 3.
По формуле Эйлера производится проверка числа построенных циклов (для самопроверки).
Определение кратчайшего пути на графе методом Дейкстры
Каждой
дуге исходного графа поставим число
 .
Если некоторая дуга
.
Если некоторая дуга
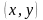 отсутствует, то положим
отсутствует, то положим
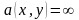 .
Будем называть число
длиной
дуги
,
хотя это число можно интерпретировать,
как соответствующие затраты или весовой
коэффициент.
.
Будем называть число
длиной
дуги
,
хотя это число можно интерпретировать,
как соответствующие затраты или весовой
коэффициент.
Рассмотрим алгоритм, который определяет путь из s в вершину t и который имеет минимальную длину. В этом алгоритме считается, что все дуги графа имеют положительную длину. Алгоритм включает в себя 3 этапа:
Все вершины и дуги не окрашены. Каждой вершине присваивается число
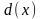 ,
равное кратчайшему пути из вершины
s
в вершину х,
который включает только окрашенные
вершины. Положим
,
равное кратчайшему пути из вершины
s
в вершину х,
который включает только окрашенные
вершины. Положим
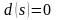 и
и
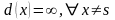 .
В этом случае окрашиваем s,
считая
.
В этом случае окрашиваем s,
считая
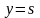 ,
где у
– последняя окрашенная вершина.
,
где у
– последняя окрашенная вершина.Для каждой неокрашенной вершины x пересчитать величину по следующей формуле
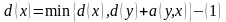 .
Если все
.
Если все
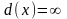 для неокрашенных вершин х
- необходимо закончить процедуру
алгоритма, так как в исходном графе
отсутствуют пути из вершины s
в неокрашенные вершины, иначе - окрасить
ту из вершин х,
для которой величина d(x)
является наименьшей, кроме того,
окрасить дугу, ведущую в выбранную на
данном шаге вершину х.
Положить
для неокрашенных вершин х
- необходимо закончить процедуру
алгоритма, так как в исходном графе
отсутствуют пути из вершины s
в неокрашенные вершины, иначе - окрасить
ту из вершин х,
для которой величина d(x)
является наименьшей, кроме того,
окрасить дугу, ведущую в выбранную на
данном шаге вершину х.
Положить
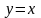 .
.Если
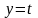 ,
то мы заканчиваем процедуру. Кратчайший
путь из вершины s
в вершину
t
найден. В противном случае вернуться
к шагу 2.
,
то мы заканчиваем процедуру. Кратчайший
путь из вершины s
в вершину
t
найден. В противном случае вернуться
к шагу 2.
Заключение:
Когда окрашивается некоторая вершина, то окрашивается и некоторая дуга, заходящая в эту вершину. Окрашенные дуги не могут образовывать в исходном графе цикла, так как в алгоритме не может окрашиваться дуга, концевые вершины которой уже окрашены.
Если кратчайшему пути из s в вершину t принадлежит вершина у, то часть этого пути, заключенная между х и у, является кратчайшим путем между этими вершинами.
Для того чтобы определить кратчайшие пути из вершины s во все вершины исходного графа, процедуру алгоритма следовало бы продолжать до тех пор, пока все вершины графа не были бы включены в ориентированное дерево кратчайших путей.
