Конденсация графа

Процедуру, связанную с построением сильных компонент можно сделать более удобной с использованием матриц R и Q.

-поэлементное умножение матриц

Тогда видно, что строка x_i , матрицы содержит единицы только в тех столбцах x_j, для которых выполняется условие: вершины x_i и x_j взаимодостижимы. В других местах строки x_i стоят нули.

Базы и антибазы

База В графа есть множество вершин, из которых достижима любая вершина графа, и которые являются минимальными в том смысле, что не найдется собственного подмножества В, обладающего таким свойством достижимости.

Если обозначить 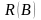множество вершин, достижимых из вершин множества В, то есть , то В является базой тогда и только тогда, когда и .

Базой является такое множество вершин графа, которое удовлетворяет условиям:

1. Каждая вершина графа G достижима хотя бы из одной вершины множества B.

2. Во множестве В нет вершины, которая достижима из других вершин множества В.

В любом графе без циклов существует единственная база. Она состоит из таких вершин графа, полустепени захода которых равны 0.

В данном примере, глядя на конденсацию, определим вершины графа, полустепени захода которых равны 0.

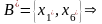базы графа G можно строить так: из каждой вершины базы B^* конденсации графа G^* необходимо взять по одной вершине.

, где m- число вершин множества в базе B^* конденсации графа G^*.

Если , то базой В является произвольное множество , где

В нашем примере:

Антибаза 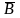есть множество всех вершин графа G, таких что 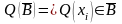, а для любых .

Антибаза есть такое минимально возможное множество вершин, что какова бы ни была вершина графа G , из нее достижима некоторая вершина в антибазе.

Таким образом, антибаза конденсации 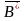есть множество вершин в графе G^*, полустепени исхода которых равны 0. Антибазы исходного графа G строятся из антибазы конденсации графа G^* путем выбора по одной вершине каждой вершине множества антибазы .

В нашем примере:

Построение компонент связности в неориентированном графе

Алгоритм состоит из следующей последовательности шагов:

1. Bсе вершины графа не помечены ( )

2. Выбираем очередную неотмеченную вершину графа, отмечаем её и все связанные с ней вершины. Значение индекса i с помощью распространения волны отмеряем по рёбрам, идущим по уже отмеченным индексам и вершинам.

Таким образом, выделяется компонента связности. Если ещё есть неотмеченные вершины, то повторяем пункт 2, иначе выделение компонент связности закончен.

Построение компонент связности в ориентированном графе

Алгоритм состоит в сведении исходного графа к неориентированному путём преобразований, не нарушающих связность вершин графа.

Алгоритм состоит из следующих этапов:

1 . Все встречные дуги в исходном

ориентированном графе заменяем

рёбрами;

2. Если в преобразованном графе уже нет дуг, то процедура алгоритма завершена, иначе выбирается любая дуга 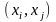и если в графе есть путь 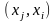, то дуга и все дуги пути заменяют рёбрами; если же пути нет, то дугу из графа удаляем, повторяя пункт 2.