
- •Изоморфизм
- •Матричное задание графа
- •Свойства матрицы смежности
- •Операции над графами
- •Достижимость и связность
- •Матрицы достижимости и контрдостижимости
- •Нахождение сильных компонент
- •Конденсация графа
- •Базы и антибазы
- •Построение компонент связности в неориентированном графе
- •Построение компонент связности в ориентированном графе
- •Система независимых циклов
- •Дерево. Остов граф
- •Процесс восстановления дерева по набору
- •Алгоритм построения произвольного остова
- •Определение минимального остова
- •Алгоритм построения системы независимых циклов графа
- •Модификация Форда
- •Алгоритмы поиска всех кратчайших путей
- •Алгоритм Флойда
- •Алгоритм Флойда
- •Алгоритм Данцига
- •Алгоритм Данцига
- •Раскраска
- •Метод построения функции Гранди на графе
- •Гамильтоновы пути, контуры и задача Коммивояжера
- •Метод Роберта и Флореса (перебор-метод для орграфов)
- •Алгоритм поиска увеличивающего пути
- •Алгоритм поиска максимального потока
- •Алгоритм Форда и Фалкерсона
- •Модификация алгоритма поиска максимального потока при нескольких источниках и стоках
- •Алгоритм поиска потока минимальной стоимости
- •Алгоритм поиска потока минимальной стоимости
- •Алгоритмы построения покрывающих деревьев
Достижимость и связность
Систему связи любой организации можно интерпретировать как граф, в котором люди представимы вершинами, а каналы связи – с дугами. При рассмотрении такой системы естественно задать вопрос: может ли информация от одного лица xi быть передана другому лицу xj, то есть, существует ли путь, идущий от вершины xi к вершине xj? Если такой путь существует, то говорят, что вершина xj достижима из вершины xi. Можно также интересоваться достижимостью на таких путях, длины которых не превосходят заданной величины.
Матрицы достижимости и контрдостижимости
Задан граф G (X, Г)
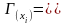 – множество вершин,
достижимых из вершины хi
на путях длиной 1.
– множество вершин,
достижимых из вершины хi
на путях длиной 1.

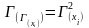 -
множество вершин, достижимых из вершины
хi
на путях длиной 2.
-
множество вершин, достижимых из вершины
хi
на путях длиной 2.
 - множество вершин,
которые достижимы из вершины хi
с использованием путей длины Р.
- множество вершин,
которые достижимы из вершины хi
с использованием путей длины Р.
Т.к. любая вершина графа G, которая достижима из вершины хi, может быть достижима с использованием пути (или путей) длиной 0 или 1 или 2 или ... или Р, то множество вершин, достижимых из хi, можно представить в виде:
 (1)
(1)
 – множество может
быть получено последовательным
выполнением операций объединения (1)
до тех пор, пока текущее множество не
будет увеличиваться по размеру при
очередной операции объединения.
– множество может
быть получено последовательным
выполнением операций объединения (1)
до тех пор, пока текущее множество не
будет увеличиваться по размеру при
очередной операции объединения.
Число объединений, которые необходимо выполнить зависит от графа, но число Р меньше числа вершин графа, следовательно, матрицу достижимости R можно построить следующим образом:
1. Находим достижимость множества для всех вершин графа, используя формулу (1);
2.
Полагаем, что
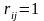 ,
если
,
если
 и
и
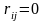 ,
если
,
если
 .
.
Матрица контрдостижимости Q определяется следующим образом:
1.
 ,
если из вершины хj
можно достигнуть в вершину хi;
,
если из вершины хj
можно достигнуть в вершину хi;
2.
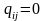 ,
если из вершины хj
нельзя достигнуть в вершину хi.
,
если из вершины хj
нельзя достигнуть в вершину хi.
Аналогично
построению достижимости множества
с помощью формулы (1) можно построить
множество
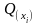 следующим образом:
следующим образом:
 (2).
(2).
Для данного графа:
 (как бы делаем
возврат назад).
(как бы делаем
возврат назад).
Операция объединения выполняется слева направо до тех пор, пока очередная операция объединения не перестанет изменять текущее множество .
Из приведенного определения следует, что столбец матрицы Q совпадает со строкой матрицы R, т.е. Q = RТ.
Пример: найти матрицу достижимости и контрдостижимости для данного графа
Построение матрицы достижимости:
Т.к.
является множеством вершин, достижимых
из хi,
а
 является множеством вершин, из которых
можно достигнуть в хj,
то пересечение
является множеством вершин, из которых
можно достигнуть в хj,
то пересечение
 есть множество таких вершин, каждая
из которых принадлежит, по крайней
мере, одному пути, идущему из вершины
хi
в вершину хj.
Эти вершины называются существенными
относительно двух конечных вершин,
идущих из вершины хi
в вершину хj.
Все остальные вершины
есть множество таких вершин, каждая
из которых принадлежит, по крайней
мере, одному пути, идущему из вершины
хi
в вершину хj.
Эти вершины называются существенными
относительно двух конечных вершин,
идущих из вершины хi
в вершину хj.
Все остальные вершины
 являются несущественными или избыточными,
поскольку их удаление не влияет на путь
из хi
в хj.
являются несущественными или избыточными,
поскольку их удаление не влияет на путь
из хi
в хj.
Нахождение сильных компонент
Подграф называется собственным, если он отличен от самого графа. Граф (орграф) называется связным (сильно связным), если для любых его вершин хi и хj существует маршрут (путь), соединяющий хi и хj. Орграф называется односторонне связным, если для любых его вершин, по крайней мере, одна достижима из другой.
Компонентой связности (сильной связности) графа G (орграфа) называется его связным (сильно связным) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (орграфа).
У графа на рисунке а) 3 компоненты связности. У ориентированного графа на рисунке б) 3 компоненты сильной связности, показанные на рисунке в).
Поскольку в сильно связном графе произвольная вершина xj достижима из любой другой вершины xi, то в ориентированном графе существует одна и только одна сильная компонента, содержащая данную вершину xi. Действительно, если бы вершина xi принадлежала двум или большему числу сильных компонент, то существовал бы путь из любой вершины сильной компоненты в произвольную вершину другой сильной компоненты, следовательно, что объединение этих сильных компонент было бы сильно связным графом, что противоречит определению сильной компоненты.
Если вершина xi
является
одновременно начальной и конечной
вершиной пути, то множество вершин
совпадет с пересечением
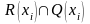 .
.
Поскольку все промежуточные вершины цикла достижимы из xi и, кроме того, из каждой такой вершины достижима вершина xi, то все эти вершины взаимодостижимы.
Множество , которое может быть построено с помощью формул: , однозначно определяет сильную компоненту графа, содержащую вершину xi .
Если все эти
вершины удалить из графа G(X,Г),
то в оставшемся
порождённом подграфе:
 ,
то можно таким образом выделить новую
сильную компоненту, содержащую вершину
,
то можно таким образом выделить новую
сильную компоненту, содержащую вершину
 .
.
Эту процедуру можно повторять до тех пор, пока все вершины графа не будут сгруппированы в соответствующие сильные компоненты графа G.
После завершения этой процедуры граф G будет разбит на сильные компоненты.
Пусть G*=G(X*,Г*) такой, что каждая его вершина представляет собой множество вершин некоторой сильной компоненты графа G.
Дуга (xi*,xj*)
в графе G*
существует тогда и только тогда, когда
в графе G
существует дуга (xi,xj),
такая что
 ,
a
,
a
 .
.
Граф G* называется конденсацией графа G. Конденсация G* не содержит циклов, поскольку наличие цикла означает, что любые вершины этого цикла взаимодостижимы, а поэтому совокупность всех вершин цикла принадлежит некоторой сильной компоненте в графе G* и, следовательно, содержится в сильной компоненте графа G, что противоречит определению конденсации, в силу которого вершины из G* соответствуют сильным компонентам графа G.
