Алгоритм поиска потока минимальной стоимости

1. (Задание начальных условий)

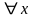1. Каждой дуге принять значение . Кроме того, положить (р(х) – вершинные числа).

2. (Выявление дуг, в которых допускается изменение потока)

Сформировать множество I, включив в него дуги , для которых выполняется и < .

1. Сформировать множество R, включив в него дуги , для которых выполняется и 0< .

2. Сформировать множество N, включив в него дуги, не вошедшие ни в I, ни в R.

На следующих этапах выполнения алгоритма изменение потока будет допускаться только в дугах, которые принадлежать I или R. Следовательно, потоки могут изменяться только в тех дугах, для которых выполняется условие .

3. (Изменение потока)

   3. Применить алгоритм поиска максимального потока к исходу сети при найденном на шаге 2 распределении дуг на множества I, R, N.

Выполнение данного алгоритма заканчивается либо тогда, когда оказывается, что из вершины s в вершину t уже передано единиц потока, либо тогда, когда выясняется, что при текущем разбиении дуг на множества I, R, N полученный поток максимален.

В первом случае – закончить выполнение алгоритма. Полученный поток заданной суммарной величины является потоком минимальной стоимости.

Во втором - случае проверить, не является ли полученный поток максимальным в исходном графе. Это осуществляется путём использования разреза, определяемого по окончании процедуры окрашивания в соответствии с алгоритмом поиска увеличивающего пути.

Поток является максимальным только в том случае, когда указанный разрез является насыщенным, в противном случае перейти к шагу 4.

4. (Изменение вершинных чисел)

   4. Исходной информацией для выполнения данного шага являются результаты окрашивания вершин в алгоритме поиска увеличивающего пути.

   5. Увеличить на +1 вершинные числа р(х) для всех неокрашенных вершин. При этом обязательно увеличится число , поскольку вершина t является неокрашенной. Затем перейти к шагу 2.

Замечание:

Множество дуг, исключение которых из графа увеличивает число его компонент, называется разрезом. Разрез, который не содержит в качестве собственного подмножества никакого другого разреза, называется простым разрезом.

Алгоритмы построения покрывающих деревьев

Рассмотрим граф G(X,E), в котором направление дуг не задаётся (т.е. это неориентированный граф). Предположим, что каждому ребру этого графа приписан вес . Определим вес покрывающего дерева, как сумму весов составляющих его рёбер.

6