Алгоритм поиска увеличивающего пути

1. Определить состав множеств N, I, R. Дуги множества N из дальнейшего рассмотрения исключить. Окрасить вершину s.

2. Окрашивать дуги и вершины в соответствии с приводимыми правилами до тех пор, пока либо не будет окрашена вершина t, либо окраска новых вершин станет невозможной.

Правила окрашивания вершины y и дуги (x, y) при уже окрашенной вершине x состоят в следующем:

а) если дуга (х, у) принадлежит I, то окрашивается вершина у и дуга (х, у);

б) если дуга (у, х) принадлежит R, то окрашивается вершина у и дуга (у, х);

в) в противном случае окрашивание дуги (х, у) и вершина у не производится.

В случае окрашивания вершины t в графе находится единственный путь из вершины s в вершину t, включающий окрашенные дуги. Этот путь является увеличивающим. Если вершина t не окрашивается, то в графе нет увеличивающего пути.

Алгоритм поиска максимального потока

Задача о максимальном потоке состоит в поиске способов пересылки максимального количества единиц потока из источника в сток при условии отсутствия превышения пропускных способностей дуг исходного графа.

Будем через 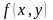обозначать количество единиц потока, прошедших по дуге .

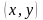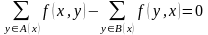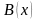При любом потоке из вершины s в вершину t количество единиц, выходящих из любой вершины x должно быть равно количеству единиц, входящих в эту вершину, то есть (1) , где ― множество вершин y , для которых в исходном графе существует дуга , а ― множество вершин y, для которых в исходном графе существует дуга 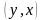. Кроме того, количество единиц потока, проходящих по каждой дуге , не должно превышать пропускной способности этой дуги: 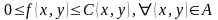(2), где A - это множество дуг графа.

Суммарное число единиц потока, выходящих из источника, должно быть равно суммарному числу единиц потока, входящих в сток. Если указанное число обозначить через 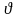, то это условие можно представить так:

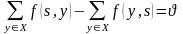(3)

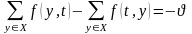(4)

Любой поток из вершины s в вершину t должен удовлетворять условиям (1-4).

Задача о максимальном потоке может быть сформулирована так: «Найти поток, который удовлетворяет условиям (1-4) и максимизирует величину ». Для решения этой задачи Фордом и Фалкерсоном был предложен следующий алгоритм.

Алгоритм Форда и Фалкерсона

1. Выбрать любой начальный поток из вершины s в вершину t , то есть любой набор вершин , удовлетворяющий соотношениям (1-4). Можно, например, положить для всех дуг , что .

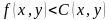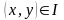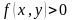2. Для всех дуг проделать следующее: если , то положить и считать дугу ; если , то положить 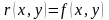и считать дугу .

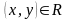3. На множества I и R , сформированных на шаге 2 исходному графу, применить алгоритм поиска увеличивающего пути. Если при этом путь, который увеличивает поток, найти не удаётся, то заканчиваем процедуру алгоритма (текущий поток - максимальный), в противном случае надо осуществить максимально возможное увеличение потока вдоль найденного увеличивающего пути, а затем идти на шаг 2.