Гамильтоновы пути, контуры и задача Коммивояжера

Гамильтонов путь в графе – это путь, проходящий через каждую его вершину один и только один раз.

Гамильтонов контур – это контур, проходящий через каждую вершину (за исключением начальной или конечной), которая совпадает один и только один раз.

Рассмотрим две задачи:

1. Дан орграф G. Требуется найти Гамильтонов контур, если он существует.

2. Дан полный орграф G, дугами которого приписаны произвольные веса C = {C_ij}. Найти такой Гамильтонов контур, который имеет наименьший общий вес.

Эту задачу называют задачей Коммивояжера.

Замечание:

Если заданный орграф G неполный, то его можно рассматривать как полный орграф, приписывая отсутствующим дугам бесконечно большой вес.

Необходимо сделать n деталей, используя один и тот же станок. При переходе от производства детали i к детали j необходимо на перенаватку станка затратить время {C_ij}. В частном случае С = 0.

Ставится задача нахождений такой последовательной обработки деталей, которая не требует перенаватки станка.

Для решения этой задачи строят граф G, вершины которого являются деталями, а существование дуги (i, j) означает, что при переходе от детали i к детали j не требуется перенаватки станка.

Решение задачи существует тогда, когда построенный граф будет иметь Гамильтонов контур.

Если предыдущая задача не имеет решения, то решаем задачу определения такой

Транспортные задачи связаны с объездом рядов пунктов и возвращением в исходный.

Задачи соединения отдельных пунктов электро-газоснабжения.

В настоящее время нет простых критериев или алгебраических методов, позволяющих выяснить: существует или нет в произвольном графе G Гамильтонов контур.

Существующие алгебраические методы определения Гамильтоновых контуров из-за большого времени работы и объёма памяти не могут быть применимы к задачам с более чем 20 вершинами.

Метод Роберта и Флореса (перебор-метод для орграфов)

Метод работает с путём, непрерывно продлеваемым до тех пор, пока либо получим Гамильтонов контур, либо ясно, что мы его не получим.

Строят M = {m_ij} k×n, где n – число вершин, k – наибольшая полустепень исхода вершины. Элемент m_ij представляет собой вершину (например (x, q)), для которой в графе G существует дуга (x_j, x_q). Вершины (x, q) во множестве Г(x_j) можно упорядочить произвольно, образовав элементы j-ого столбца матрицы М.

Некоторая вершина (например, x₁) выбирается в качестве отправной и образуется первый элемент множества S, в котором хранятся уже найденные вершины строящегося пути. К множеству S добавляется первая вершина (например, x₂) из столбца x₁, затем к множеству S добавляется первая возможная вершина (пусть x₃) из столбца x₂ и т.д.

Под “возможной” вершиной мы понимаем вершину, ещё не принадлежащую множеству S.

Существует две причины, препятствующие включению некоторой вершины на шаге r в S:

1. B столбце x_r нет возможной вершины;

2. Путь, определяемый последовательностью вершин из множества S, имеет длину (n-1), т.е. является Гамильтоновым.

В этом случае:

1. В графе G существует дуга (x_r, x₁) и поэтому Гамильтонов контур может быть найден;

2. Дуга (x_r, x₁) не существует и не может быть получен Гамильтонов контур.

В случае 1 и 2б) следует прибегнуть к операции возвращения, 2а) – можно распечатать результат. Возвращение состоит в удалении последней включённой вершины x_r из множества S.

и добавлений к множеству S первой возможной вершины следующей за х_r в столбце х_r-1 матрицы М.

Если не существует никакой возможной вершины в столбце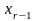 , делается следующий шаг возвращения и т.д.

Поиск заканчивается в том случае, когда множество S состоит только из вершины x₁ и не существует никакой возможной вершины в столбце х₁, которую можно добавить к множеству S, потому что следующий шаг возвращения делает множество S пустым. Таким образом, можно найти все Гамильтоновы контуры.