
- •2. Определение матриц. Виды матриц.
- •1. Математическая модель. Этапы математического моделирования.
- •3. Транспонирование матриц. Свойства.
- •5. Произведение матриц. Возведение матриц в степень. Свойства произведения.
- •6. Вычисление определителей 2-го и 3-го порядков. Свойства определителей.
- •7. Минор и их алгебраическое дополнение элемента матрицы.
- •8. Вычисление определителей n-го порядка разложением по ряду и приведением к треугольному виду.
- •9. Определение обратной матрицы. Условие существования обратной матрицы. Формула нахождения обратной матрицы.
- •11. (Только практика) Способы вычисления ранга.
- •12.Сформулировать элементарные преобразования матриц. Определение эквивалентных матриц.
- •15.(Только практика) Решение системы матричным способом.
- •16.(Только практика) Решение системы методом Крамера.
- •17.(Только практика) Решение системы методом Гаусса.
- •18.Совместная и несовместная система. Критерий совместности системы. Правила практического разыскания решений.
- •19.(Только практика) Алгоритм решения произвольной системы линейных уравнений.
- •20.Определение однородной системы уравнений. Сформулировать теорему об условии существования нетривиального решения. Что называется фундаментальной системой решения?
- •21.Определение вектора, противоположного вектора, длины вектора, нулевого и единичного векторов, коллинеарных. Равных и компланарных векторов.
- •22.Линейные операции над векторами.
- •23.Формула разложения вектора по ортам координатных осей. Координаты вектора. Выражение линейных операций над векторами в координатах.
- •24.Формула деления отрезка в заданном отношении.
- •25.Определение скалярного произведения векторов. Выражение скалярного произведения через координаты.
- •26. Как найти угол между векторами?
- •27.Определение n-мерного вектора и его координат. Определение векторного пространства. Как найти сумму, произведение на число, скалярное произведение и длину n-мерных векторов?
- •28.Линейная комбинация векторов. Определение линейно зависимой и независимой системы.
- •29.Уравнения прямой на плоскости (6 видов).
- •30.Угол между прямыми и условия параллельности и перпендикулярности двух прямых.
- •31.Расстояние от точки до прямой.
- •32.Уравнения плоскости в пространстве (4 вида).
- •33.Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.
- •34.Расстояние от точки до плоскости.
- •35.Уравнения прямой в пространстве (4 вида)
- •40.Определение гиперболы и се каноническое уравнение. Исследование формы гиперболы. Асимптоты гиперболы. Дополнительные сведения о гиперболе.
- •41.Парабола и ее каноническое уравнение. Исследование формы параболы.
- •43.Определение предела последовательности и его геометрическая интерпретация.
- •44.Свойства сходящихся последовательностей.
- •45.Определение, способы задания и свойства функции.
- •46.1)Определение предела функции в точке 2)Предел функции при х→∞ 3)Односторонние пределы.
- •47.Бесконечно малые и бесконечно большие функции и их свойства.
- •48.Основные свойства пределов.
- •49.Замечательные пределы (1-й - с доказательством).
- •50.Определение функции непрерывной в точке, в интервале и на отроке. Точки разрыва.
- •51.Определение производной функции в точке. (производная – это скорость).
- •52. Механический, геометрический и экономический смысл производной.
- •53.Таблица производных элементарных функций. Правила вычисления производных.
- •54.Дифференциал функции и его геометрическая интерпретация. Свойства дифференциала.
- •55.Производные и дифференциалы высших порядков.
51.Определение производной функции в точке. (производная – это скорость).
Пусть
функция
определена на некотором интервале
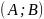 и
– некоторая фиксированная точка этого
интервала.
и
– некоторая фиксированная точка этого
интервала.
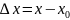 – приращение аргумента.
– приращение аргумента.
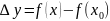 – приращение функции. Составим отношение
– приращение функции. Составим отношение
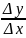 и рассмотрим предел этого отношения
при
и рассмотрим предел этого отношения
при
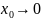 .
.
Производной
функции
в точке
называется предел отношения приращения
функции к приращению аргумента, когда
последний стремится к нулю. Обозначается
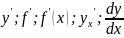 .
По определению:
.
По определению:
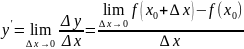 .
.
Функция , имеющая производную в каждой точке интервала называется дифференцируемой, операция нахождения производной называется дифференцированием.
52. Механический, геометрический и экономический смысл производной.
Механический:
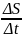 – средняя скорость.
– средняя скорость.
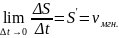 – мгновенная скорость. Обобщая можно
сказать, что если функция
описывает какой-либо физический процесс,
то производная функции есть скорость
протекания этого процесса.
– мгновенная скорость. Обобщая можно
сказать, что если функция
описывает какой-либо физический процесс,
то производная функции есть скорость
протекания этого процесса.
Геометрический:
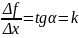 – угловой коэффициент секущей.
– угловой коэффициент секущей.
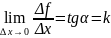 – угловой коэффициент касательной.
– угловой коэффициент касательной.
Экономический:
пусть
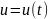 выражает количество производимой
продукции u
за время t.
выражает количество производимой
продукции u
за время t.
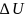 – изменение количества продукции за
период времени t.
– изменение количества продукции за
период времени t.
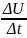 – средняя производительность труда
за время
– средняя производительность труда
за время
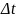 .
.
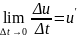 - производительность труда в момент
времени
- производительность труда в момент
времени
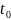 .
.
53.Таблица производных элементарных функций. Правила вычисления производных.
При вычислении производных нужно знать 1. Таблицу производных; 2. Правило производных.
1.
c’
= 0; 2. X’
= 0; 3.
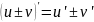 ;
4.
;
4.
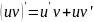 и
и
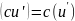 ;
5.
;
5.
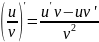 ;
6.
;
6.
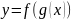 -
-
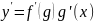 .
.
54.Дифференциал функции и его геометрическая интерпретация. Свойства дифференциала.
Пусть
производная
имеет в точке x
производную отличную от нуля.
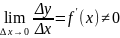 ,
то есть
,
то есть
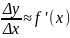 при
при
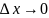 .
Воспользуемся следующим утверждением:
если функция
имеет предел, то
,
.
Воспользуемся следующим утверждением:
если функция
имеет предел, то
,
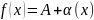 ,
где
,
где
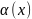 – бмф. Тогда можно записать, что
– бмф. Тогда можно записать, что
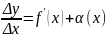 при
и
– бмф. Первое слагаемое правой части
при
и
– бмф. Первое слагаемое правой части
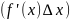 называется главной частью приращения
называется главной частью приращения
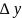 .
.
Дифференциалом
функции
в точке x
называется главная часть ее приращения,
равная произведению производной функции
на приращение аргумента и обозначается
dy
или df.
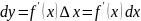 .
.
Геометрический
смысл дифференциала функции: Дифференциал
функции
в точке x
равен приращению ординаты касательной
к графику функции в этой точке, когда
x
получит приращение
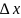 .
.
Свойства дифференциала:
1.
dc=0; 2. D(cu)=cdu; 3. D(u+v)=du+dv; 4. D(uv)=vdu+udv; 5.
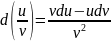 ;
6. Если
;
6. Если
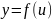 и
и
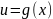 – дифференциал функции, образующей
сложную функцию
,
то
– дифференциал функции, образующей
сложную функцию
,
то
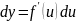 .
Дифференциал сложной функции определяется
формулой
.
Дифференциал сложной функции определяется
формулой
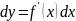 .
Это свойство называется инвариантностью
(неизменностью) формы дифференциала.
.
Это свойство называется инвариантностью
(неизменностью) формы дифференциала.
55.Производные и дифференциалы высших порядков.
Производная
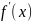 сама является функцией, которая также
может иметь производную. Производной
n-ого
порядка называется производная от
производной (n-1)-ого
порядка. Обозначается
сама является функцией, которая также
может иметь производную. Производной
n-ого
порядка называется производная от
производной (n-1)-ого
порядка. Обозначается
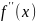 – 2-ого порядка,
– 2-ого порядка,
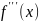 – 3-его порядка,
– 3-его порядка,
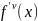 или
или
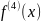 – 4-ого порядка,
– 4-ого порядка,
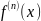 – производная n-ого
порядка. Если производная 1-ого порядка
от пути есть скорость, то
– производная n-ого
порядка. Если производная 1-ого порядка
от пути есть скорость, то
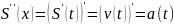 – ускорение точки в момент времени
.
– ускорение точки в момент времени
.
Пусть
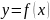 – дифференцируемая функция, а x
– независимая переменная. Тогда ее
1-ый дифференциал
также есть функция и можно найти
дифференциал этой функции. Дифференциал
от дифференциала функции
называется дифференциалом 2-ого порядка
и обозначается
– дифференцируемая функция, а x
– независимая переменная. Тогда ее
1-ый дифференциал
также есть функция и можно найти
дифференциал этой функции. Дифференциал
от дифференциала функции
называется дифференциалом 2-ого порядка
и обозначается
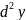 или
или
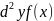 .
.
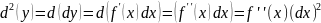 .
Аналогично определяется дифференциал
любого порядка. Дифференциал n-ого
порядка называется дифференциалом от
дифференциала (n-1)-ого
порядка.
.
Аналогично определяется дифференциал
любого порядка. Дифференциал n-ого
порядка называется дифференциалом от
дифференциала (n-1)-ого
порядка.
