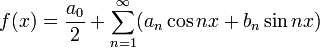- •Вопросы к государственному экзамену Дисциплина «Моделирование систем»
- •Понятие модели системы.
- •Определение понятия «моделирование».
- •Использование гипотез и аналогий в исследовании систем.
- •Отличие использования метода моделирования при внешнем и внутреннем проектировании систем
- •Сущность системного подхода к моделированию систем.
- •2 Вариант
- •Процесс функционирования системы.
- •Классификационные признаки видов моделирования систем.
- •Математическое моделирование систем.
- •9. Особенности имитационного моделирования систем.
- •Метод статистического моделирования.
- •11.Критерии эффективности моделирования систем на эвм.
- •Определение математической схемы.
- •13. Экзогенные и эндогенные переменные в модели объекта.
- •14. Закон функционирования системы.
- •15. Понятие алгоритма функционирования.
- •16. Определение статической и динамической моделей объекта.
- •Типовые схемы, используемые при моделировании сложных систем и их элементов.
- •Условия и особенности использования при разработке моделей систем различных типовых схем.
- •Концептуальная модель системы.
- •Группы блоков выделяемые при построении блочной конструкции модели системы.
- •Сущность статистического моделирования систем.
- •Способы генерации последовательностей случайных чисел используемые при моделировании на эвм.
- •Существующие методы проверки качества генераторов случайных чисел.
- •Характерные особенности машинного эксперимента по сравнению с другими видами экспериментов.
- •Виды факторов в имитационном эксперименте с моделями систем.
- •Цель стратегического планирования машинных экспериментов.
- •Цель тактического планирования машинных экспериментов.
- •Точность и достоверность результатов моделирования систем.
- •Сущность фиксации и обработки результатов при статистическом моделировании систем.
- •Место имитационных моделей при машинном синтезе систем.
- •Способы построения моделирующих алгоритмов q –схем.
- •Синхронный и асинхронный моделирующие алгоритмы q –схем.
- •Суть структурного подхода при моделировании систем на базе n –схем.
- •34. Особенности формализации процессов функционирования систем на базе а – схем.
- •Информационная модель системы.
- •Характерные черты эволюционных моделей систем.
- •37.Роль эталонной модели в контуре управления.
- •38.Виды моделей, используемых для принятия решений.
- •39.Суть адаптации применительно к системам управления различными объектами.
- •40.Требования, предъявляемые к модели, реализуемой в реальном масштабе времени.
- •41.Какой процесс, протекающий в системе, называется Марковским?
- •42.Какой процесс называется процессом с дискретным состоянием?
- •43.Какой процесс называется процессом с непрерывным временем?
- •44. Что такое поток событий?
- •45. Что такое интенсивность потока событий?
- •Какой поток событий называется стационарным?
- •47. Какой поток событий называется ординарным?
- •48.Какой поток событий называется простейшим?
- •49.Как ведут себя смо с ограниченной очередью?
- •50.Чем отличаются динамические системы от статических?
- •51.Как выбирается частота дискретизации (теорема Котельникова)?
- •Вопрос 52. Что представляет собой динамический ряд?
- •Типы динамических рядов
- •Вопрос 53. Чем характеризуется динамическая система?
- •Вопрос 54. Что такое порядок динамической системы?
- •Вопрос 55. Что характеризуют параметры динамической системы k и t?
- •56.Передаточная функция звена первого порядка.
- •57.Передаточная функция звена второго порядка.
- •58.Переходная функцией (или переходная характеристикой) динамической системы ?
- •59.Функция Хэвисайда от времени 1[t].
- •60.Уравнение ряда Фурье и коэффициентов а0, Аi, Bi .
- •61.Процесс вычисления коэффициентов а0, Аi, Bi ряда Фурье?
- •Определение коэффициентов по методу Эйлера-Фурье.
- •62.Ряд Фурье для нечетной функции.
- •63.Ряда Фурье для четной функции.
- •64.Как вычисляется составляющие ачх (Si)?
- •65.Как вычисляется составляющие фчх (ϕi)?
- •66.Обратное преобразование Фурье для Si, ϕi.
- •67.Достоинства представления сигнала и динамической системы в виде Фурье представления при моделировании
- •68.К чему свелось моделирование прохождения сигнала через динамический объект в виде Фурье представления?
- •69.Основное уравнение динамики.
- •70.Формулой Эйлера.
- •71.Формулой Эйлера при Δt≠0.
- •72.Как изменяется t (счетчик t) и y при алгоритмической реализации расчет циклом по методу Эйлера?
- •73.Как обозначают порядок зависимости точности от величины шага?
- •74.Каков и по какой причине порядок точности у метода Эйлера?
- •75.В каких случаях численный метод обладает сходимостью?
- •Сходимость означает, что погрешность каждого последующего приближения должна быть меньше погрешности предыдущего приближения, т.Е. Погрешность приближенных значений с каждым шагом должна уменьшаться:
- •В общем случае это неравенство можно представить в виде:
- •76.Какая характеристика сходимости интересует исследователей?
- •77.Что понимается под неустойчивостью метода?
- •78.Что обеспечивает устойчивость метода?
- •79.Что обеспечивает сходимость метода?
- •80. Идея уточненного метода Эйлера.
- •Сущность другого варианта модифицированного метода Эйлера
- •Какова точность метода Рунге-Кутта?
- •Какая функция по методу Рунге-Кутта используется для построения разностной схемы интегрирования?
- •94.Что представляет собой критерий согласия Фишера и каким образом его можно применять?
- •95.Что представляет собой критерий Смирнова и каким образом его можно использовать?
- •96.Что представляет собой критерий согласия Стьюдента и как он используется?
- •97.Объясните смысл понятий: несмещенность оценки, эффективность оценки, состоятельность оценки.
- •98.Каким образом следует вбирать число реализаций опыта?
- •99.Объясните смысл понятия «мощность критерия».
- •100 Каким образом можно выбирать границы для оценки моделируемой случайной величины?
58.Переходная функцией (или переходная характеристикой) динамической системы ?
Динамические свойства линейных звеньев и систем автоматического управления в целом могут быть описаны уравнениями и графическими характеристиками. В теории автоматического применяются два типа таких характеристик – временные и частотные. Эти характеристики могут быть сняты экспериментально или построены по уравнению звена
Переходная или временная характеристика
(функция) звена
![]() представляет собой реакцию на выходе
звена, вызванную подачей на его вход
единичного, ступенчатого воздействия.
Единичное, ступенчатое воздействие
(единичная, ступенчатая функция)
представляет собой реакцию на выходе
звена, вызванную подачей на его вход
единичного, ступенчатого воздействия.
Единичное, ступенчатое воздействие
(единичная, ступенчатая функция)![]() – это воздействие, которое мгновенно
возрастает от нуля до единицы и далее
остается неизменным
– это воздействие, которое мгновенно
возрастает от нуля до единицы и далее
остается неизменным
![]()
Таким образом
![]() .
.
В случае линейной системы переходная функция играет важную роль в анализе её характеристик. В зависимости от приложения, качество системы можно оценивать по переходной функции.
59.Функция Хэвисайда от времени 1[t].
Функция Хевисайда (единичная ступенчатая функция, функция единичного скачка, включенная единица) — кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных. В нуле эта функция, вообще говоря, не определена, однако её обычно доопределяют в этой точке некоторым числом, чтобы область определения функции содержала все точки действительной оси. Чаще всего неважно, какое значение функция принимает в нуле, поэтому могут использоваться различные определения функции Хевисайда, удобные по тем или иным соображениям, например[1]
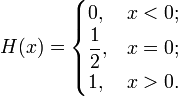
Другое распространённое определение:
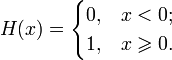
Функция Хевисайда широко используется в математическом аппарате теории управления и теории обработки сигналов для представления сигналов, переходящих в определённый момент времени из одного состояния в другое. В математической статистике эта функция применяется, например, для записи эмпирической функции распределения. Названа в честь Оливера Хевисайда.
60.Уравнение ряда Фурье и коэффициентов а0, Аi, Bi .
Пусть
функция f(x)
- интегрируемая и периодическая с
периодом 2![]() .
Коэффициенты Фурье функции f(x)
называются числа a0,a1,…an
и b0,b1,…bn,
которые находятся по формулам:
.
Коэффициенты Фурье функции f(x)
называются числа a0,a1,…an
и b0,b1,…bn,
которые находятся по формулам:
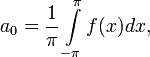
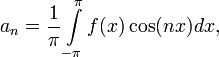
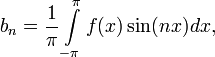
Рядом Фурье функции f (x) называют ряд вида
|
(1) |
61.Процесс вычисления коэффициентов а0, Аi, Bi ряда Фурье?
Пусть у нас уже есть функция, разложенная в тригонометрический ряд
![]()
![]()
![]() (4)
(4)
В данном разложении функция от угла х,
имеющая период
![]() разложена по косинусам и синусам углов,
кратных х.
разложена по косинусам и синусам углов,
кратных х.
Мы пришли к разложению функции в тригонометрический ряд, отправляясь от периодических, колебательных явлений и связанных с ними величин. Подобные разложения часто оказываются полезными и при исследовании функций, заданных в определенном конечном промежутке и вовсе не порожденных никакими колебательными явлениями.
Определение коэффициентов по методу Эйлера-Фурье.
существует ряд функций, которые можно
представить в виде бесконечного
тригонометрического ряда. Для того, что
бы установить возможность разложения
некоторой функции
![]() ,
имеющей период
,
имеющей период
![]() в
тригонометрический ряд вида:
в
тригонометрический ряд вида:
(4)
нужно иметь набор коэффициентов
![]()
Прием для нахождения этих коэффициентов во второй половине XVIII века был применен Эйлером и независимо от него в начале XIX века—Фурье.
Впредь будем предполагать функцию
непрерывной
или кусочно-непрерывной в промежутке
![]() .
.
Допустим, что разложение (4) имеет место.
Проинтегрируем его почленно от
![]() до
до
![]() ;
в результате получим:
;
в результате получим:
![]()
Но, как легко видеть,
 (5)
(5)
Поэтому все члены под знаком суммы будут равняться нулю, и окончательно получаем
![]() (6)
(6)
Для того чтобы найти значение коэффициента
![]() ,
умножим обе части равенства (4) на
,
умножим обе части равенства (4) на
![]() и снова проинтегрируем почленно в том
же промежутке:
и снова проинтегрируем почленно в том
же промежутке:
![]()
В виду (5)
![]() .
.

если
![]() ,
и, наконец,
,
и, наконец,
![]() (9)
(9)
Таким образом, обращаются в нуль все интегралы под знаком суммы, кроме интеграла, при котором множителем стоит именно коэффициент . Отсюда получаем:
![]()
![]()
Аналогично, умножая разложение (4) на
![]() и
затем, интегрируя почленно, определим
коэффициент при синусе:
и
затем, интегрируя почленно, определим
коэффициент при синусе:
![]()
Формулы, по которым вычисляются
коэффициенты
![]() ,
называются формулами Эйлера-Фурье, а
сами коэффициенты называются коэффициентами
Фурье для данной функции. И, наконец,
тригонометрический ряд (4), составленный
по этим коэффициентам, получил название
ряд Фурье для данной функции.
,
называются формулами Эйлера-Фурье, а
сами коэффициенты называются коэффициентами
Фурье для данной функции. И, наконец,
тригонометрический ряд (4), составленный
по этим коэффициентам, получил название
ряд Фурье для данной функции.