17. Концептуальная модель системы.

Концептуальная (содержательная) модель - это абстрактная модель, определяющая структуру моделируемой системы, свойства ее элементов и причинно-следственные связи, присущие системе и существенные для достижения цели моделирования. Иными словами, это содержательная модель, при формулировании которой используются понятия и представления предметных областей, связанных с моделью. Например, ММ формулируется на языке математики – с помощью математических структур: формул, пространственных форм и т.п.

Выделяют три вида концептуальных моделей: логико-семантические, структурно-функциональные и причинно-следственные.

Логико-семантическая модель – описание объекта в терминах соответствующих предметных областей знаний. Анализ таких моделей осуществляется средствами логики с привлечением специальных знаний.

При построении структурно-функциональной модели объект рассматривается как целостная система, которую расчленяют на отдельные подсистемы или элементы. Части системы связывают структурными отношениями, описывающими подчиненность, логическую и временную последовательность решения задач.

Причинно-следственная модель служит для объяснения и прогнозирования поведения объекта. Такие модели ориентированы на следующие моменты: 1) выявление главных взаимосвязей между подсистемами;  2) выявление определенного влияния различных факторов на состояние объекта;  3) описание динамики интересующих разработчика параметров.

Формальная модель является представлением концептуальной модели с помощью формальных языков. К таким языкам относятся математический аппарат, алгоритмические языки, языки моделирования.

Построение концептуальной модели включает следующие этапы:

1) определение типа системы;

2) описание внешних воздействий;

3) декомпозиция системы.

17. Группы блоков выделяемые при построении блочной конструкции модели системы.

Наиболее рационально строить модель функционирования системы по блочному принципу.

При этом могут быть выделены три автономные группы блоков такой модели.

• Блоки первой группы представляют собой имитатор воздействий внешней среды Е на систему S; 

• блоки второй группы являются собственно моделью процесса функционирования иссле­дуемой системы S;

• блоки третьей группы — вспомогательными и служат для машинной реализации блоков двух первых групп, а также для фиксации и обработки результатов моделирования.

Рассмотрим механизм перехода от описания процесса функци­онирования некоторой гипотетической системы к модели этого процесса [29, 35]. Для наглядности введем представление об описании свойств процесса функ­ционирования системы S, т. е. об ее концептуальной модели М_т как совокупности некоторых элементов, усло­вно изображенных квадрата­ми так, как показано на рис. 3.2, а. Эти квадраты пред­ставляют собой описание не­которых подпроцессов ис­следуемого процесса функ­ционирования системы S, воздействия внешней среды Е и т. д. Переход от описа­ния системы к ее модели в этой интерпретации сво­дится к исключению из рассмотрения некоторых второстепенных элементов описания (элемен­ты 5 — 8,39 — 41,43 — 47).

 

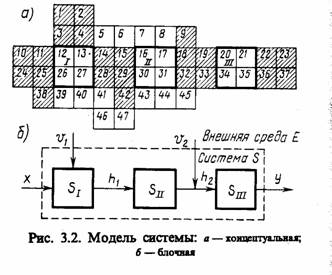
Предполагается, что они не оказывают существенного влияния на ход процессов, исследуемых с помощью модели. Часть элементов (14, 15, 28, 29, 42) заменяется пассивными связями h_l3отражающими внутренние свойства системы (рис. 3.2, б). Некоторая часть элементов (1 — 4, 10, 11, 24, 25) заменяется входными факторами х и воздействиями внешней среды v₁. Воз­можны и комбинированные замены: элементы 9, 18, 19, 32, 33 заменены пассивной связью h₂ и воздействием внешней среды Е. Элементы 22, 23,36,37 отражают воздействие системы на внешнюю средуу.

Оставшиеся элементы системы S группируются в блоки 5_t, S_a, S_m, отражающие процесс функционирования исследуемой системы. Каждый из этих блоков достаточно автономен, что выражается в минимальном количестве связей между ними. Поведение этих блоков должно быть хорошо изучено и для каждого из них постро­ена математическая модель, которая в свою очередь может содер­жать ряд подблоков. Построенная блочная модель процесса функци­онирования исследуемой системы 5 предназначена для анализа характеристик этого процесса, который может быть проведен при машинной реализации полученной модели.