§23. Гиперболоиды и конус.

Гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением , где коэффициенты А, В и С − числа разных знаков, а L – отлично от нуля. Для определенности будем считать, что А и В больше нуля, а

С – меньше нуля: A > 0, B > 0, C < 0. В зависимости от знака L имеем два типа гиперболоидов.

I. L < 0. После стандартных преобразований (§22) получим уравнение: .

Снова воспользуемся методом сечений.

Плоскости z = h поверхность пересекает по эллипсам .

С увеличением h ( или z) полуоси эллипса увеличиваются. Минимальные полуоси будут при

h = 0 , т.е. в плоскости ХОY.

В плоскостях x = h (или y = h ) получаются гиперболы . (рис.12а)

При h < a или h > a (для y − h < b или h > b ) гиперболы ориентированы противоположно.

При h = a (h = b) сечениями являются прямые. Это свидетельствует о наличии у однополосного гиперболоида прямолинейных образующих.

При a = b имеем гиперболоид вращения.

Поверхность, описываемая уравнением называется однополосный гиперболоид.

Пример. Доказать, что т. (5,4,2) принадлежит гиперболоиду и найти прямолинейные образующие, проходящие через эту точку. {1)1+1−1=1;2) l:x=pt+5,y=qt+4,z=rt+2

Подставим в уравнение: приравняем коэффициенты нулю и положим r = 1 и вторая образующая

}

II. L > 0. В этом случае уравнение будет иметь вид: .

При z = h имеем 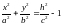, откуда сразу следует ограничение на h и, тем самым, на величину z: . В сечениях, как и в предыдущем случае будут эллипсы. При z = ±1 эллипсы вырождаются в точки (0,0,±1).

При x = h или y = h в сечениях опять получатся гиперболы, но в отличие от однополостного гиперболоида не меняющие ориентацию в зависимости от величины h (рис.12б).

При a = b получим гиперболоид вращения.

Поверхность называется двуполостным гиперболоидом.

2. Пусть теперь при тех же ограничениях на А, В и С L = 0. Уравнение примет вид:

Сечения плоскостями z = h опять будут эллипсами с увеличивающимися полуосями при возрастании модуля z, а в сечениях x = h или y = h − пересекающиеся прямые (рис.12в).

Такие поверхности называются коническими или конусами.

§24. Параболоиды.

Параболоидом называется поверхность, которая в некоторой декартовой системе координат

определяется уравнением , где коэффициенты А, В и K не равны нулю.

Возможны два случая: AB > 0 и AB < 0. Для определенности будем считать A > 0, K < 0.

1. A > 0, B > 0, K < 0. Уравнение приводится к виду .

В сечениях z = h (h > 0) получаем эллипсы , полуоси которых растут с ростом h.

В сечениях x = h и y = h − параболы 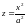и (рис.13а).

Поверхность называется эллиптическим параболоидом.

z z

х

y y

x

рис.13а рис.13б

II. A > 0, B < 0, K < 0. Уравнение имеет вид: − гиперболический параболоид.

В сечениях z = h получаются гиперболы, ориентация которых меняется при изменении знака h.

В сечениях x = h и y = h − параболы, имеющие противоположное направление ветвей (рис.13б).

Позднее, при изучении общих свойств линейных пространств, будет доказано, что никаких других поверхностей второго порядка не существует. Возможны только некоторые частные и вырожденные случаи. Любое уравнение второго порядка от трех переменных приводится к одному из рассмотренных типов.

5