Вопросы для самоподготовки.

1. На какие составляющие раскладывается сила полного давления в косозубой цилиндрической передаче?

2. Как поменять направление действия осевой составляющей в косозубой цилиндрической передаче?

3.Какова взаимосвязь между силами, приложенными к шестерне и колесу, в косозубой цилиндрической передаче?

4. Как определяется минимальная суммарная длина контактных линий в косозубой цилиндрической передаче?

5. Как определяется расчетная нагрузка в косозубой цилиндрической передаче?

6. В чем отличие формулы для оценки действующих напряжений на контактную прочность для косозубых и прямозубых цилиндрических передач?

7. Особенности расчета косозубых цилиндрических передач на изгиб.

8. Что такое эквивалентное число зубьев?

9. Какие конические передачи называют ортогональными?

10. В каких сечениях рассматривают геометрические параметры конических передач?

11. Понятие о “эквивалентной цилиндрической передаче” при расчетах конических передач.

ЛЕКЦИЯ №9

Конические передачи (продолжение

Силы, действующие в зацеплении.

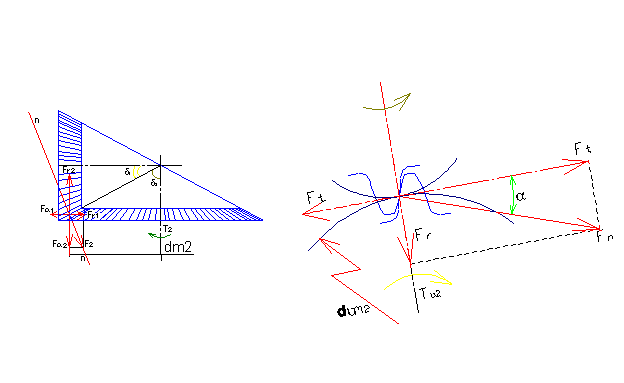
Силы, действующие в зацеплении двух конических колёс рассматриваем приложенными посередине зубчатого венца. Нормальная к зубу сила F_n действует в сечении n-n перпендикулярно к поверхностям зубьев (т.е. по направлению совпадает с линией зацепления в этом сечении).

При определении сил, действующих в зацеплении будем исходить из момента на колесе Т₂. Тогда окружная сила на среднем диаметре колеса будет:

В эквивалентной цилиндрической передаче (см. сечение n-n) по окружной силе F_n легко определяется радиальная сила F_r:

F_r=F_t*tgα

В конической передаче эта сила F_r действует по направлению n-n. Разложим эту силу по двум направлениям, направлениям, параллельным осям:

- радиальная сила на колесе.

- осевая сила на колесе.

Равные по величине, но противоположно направленные силы действуют со стороны колеса на шестерню. Эти силы на схеме показаны пунктирными линиями. Причем, окруженные силы, как на колесе, так и на шестерне по величине равны:

Таким образом, нормальная сила F_n, действующая на зубья конических колес, раскладывается на три взаимно перпендикулярные составляющие: окружную, радиальную и осевую.

Расчет на контактную прочность.

Расчет конической передачи на контактную прочность основан на предположении, что нагрузочная способность её равна нагрузочной способности эквивалентной цилиндрической передачи. Причем, ширина колес эквивалентной цилиндрической передачи принимается равной ширине зубчатого венца конической передачи. Поэтому, при выводе расчетных формул, при выводе расчета ширине зубчатого венца конической передачи. Поэтому, при выводе расчетных формул для расчета конической передачи на контактную прочность можно воспользоваться формулами, полученными для цилиндрических зубчатых передач. Только в этих формулах величины А, U и Т нужно будет соответственно заменить А ,U и Т .

Так, если оба колеса стальные и угол =20 , можно написать:

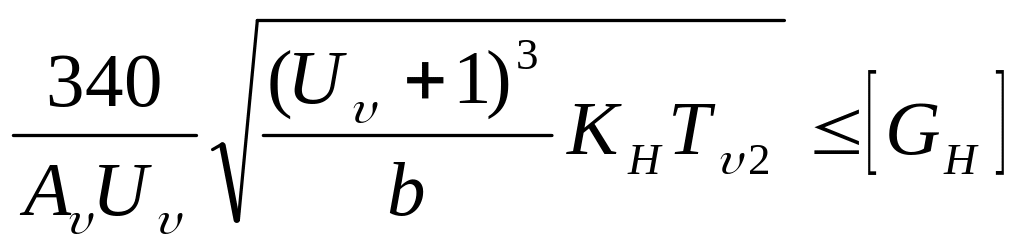= (1)

Установим сначала зависимость между моментами на коническом колесе Т и эквивалентом цилиндрическом колесе Т . При одинаковой нагрузкой способности добавление между зубьями эквивалентной цилиндрической передачи должно быть равно давлению между зубьями рассчитываемой конической передачи. Тогда можно написать:

Отсюда: T

Теперь, подставим в формулу (1):

a =(Re-0,5b) и вводя в рассмотрение безразмерный параметр К , получаем формулы для проверочного и проектного расчетов конических передач на контактную прочность:

(2)

Re= (3)

В формулах (2) и (3)

Re и b – в мм,

Т - в Н. Мм,

и - в

К (при расчете по формуле (3) задаемся сами)

Коэффициент нагрузки К в случае конических зубчатых передач определяется примерно также как и в случае цилиндрических передач. Причем, при выборе коэффициента динамической нагрузки К окружная скорость в зацеплении определяется на среднем диаметре конических колес.

Допускаемое контактное напряжение определяется согласно рекомендациям, приведенным для цилиндрических передач.

Расчет зубьев на изгиб.

При выводе расчетных формул для расчета зубьев конических передач по изгибным напряжениям следует исходить из следующего:

1.Пересечение осей валов затрудняет размещение опор. Одно из конических Колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба. Поэтому считается, что нагрузочная способность конической передачи (по опытным данным) составляют лишь 85% по сравнению с цилиндрической, что учитывается при оценке допускаемых напряжений.

2.Размеры поперечных сечений зуба конического колеса изменяются пропорционально расстоянию этих сечений от вершины конуса.

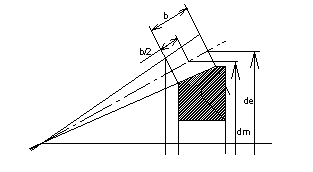
Все поперечные сечения геометрически подобны. При этом погонная нагрузка «q» распределяется неравномерно по длине зуба, меняясь пропорционально жесткости зуба. Считается, что погонная нагрузка «q» меняется по закону треугольника, вершина которого совпадает с вершиной делительного конуса, и что изгибные напряжения одинаковы по всей длине зуба. Это позволяет вести расчет для любого сечения, например, приняв за расчетное среднее сечение зуба. Поэтому по аналогии с прямозубой цилиндрической передачей можно написать:

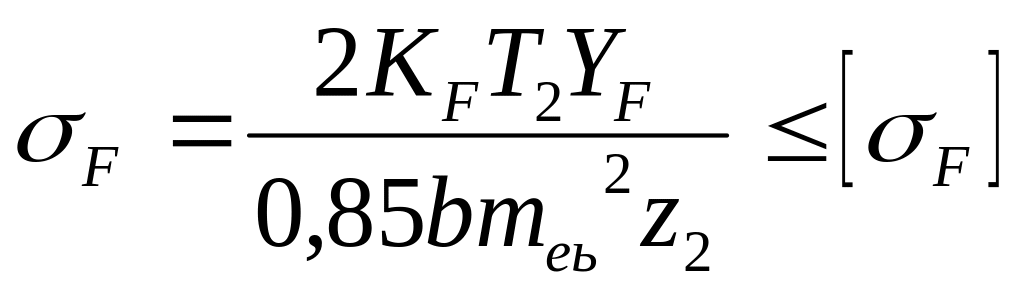(4)

Формула (4) удобна при проверочных расчетах зубьев конической передачи по изгибным напряжениям. Вводя безразмерный коэффициент ширины зубчатого венца , получаем формулу для проектного расчета:

m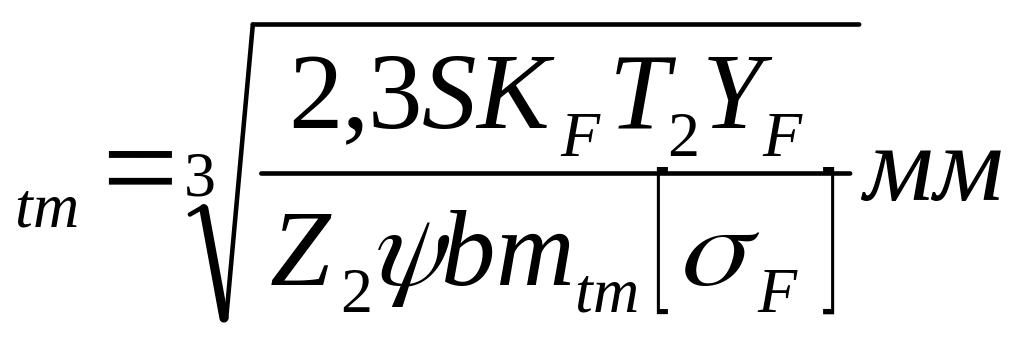 (5)

В формулах (4) и (5):

B и m мм,

Т - в Н. Мм,

[σ_F] и σ_F – в Н/мм²

где: К

Некоторые особенности расчета по формулам (4) и (5) в зависимости от материалов шестерки и колеса в случае конической передачи остаются такими же, какие они были в случае цилиндрических передач.

Допускаемое изгибное напряжение определяется согласно рекомендациям, приведенных для цилиндрических передач, с учетом пониженной нагрузочной способности конических передач умножением на 0,85.

Червячные передачи.

Червячные пары применяются в передачах между валами, оси которых в пространстве скрещиваются.

Достоинства червячных передач:

А) Компактность и возможность осуществления в одной паре больших передаточных чисел. Обычно в червячных передачах U . В силовых червячных передачах U=8…100. в передачах малой мощности (в приборах) иногда до U=500…1000.

Б) Плавность и бесшумность работы.

Недостатки червячных передач:

А) Низкий кпд, следовательно, большие потери мощности (особенно в передачах с однозаходным червяком).

Б) Необходимость применения для червячных колес дорогостоящих антифрикционных материалов (например, бронзы).

Материалы.

Говоря и Материалах, применяемых для червячного колеса и червяка, следует помнить, что червячная передача характеризуется большим относительным скольжением между элементами кинематической пары, т.е. между поверхностями витком червяка и зубьев червячного колеса. Отсюда необходимость применения материалов, обладающих низким коэффициентом трения.

Для червячного колеса (или его венца) обычно применяются:

1. при скорости скольжения > 4 - оловянистые бронзы разных марок, например; БрОФ10-1, БрОНФ10-1-1 и др.

2. при скорости скольжения безоловянистые бронзы и латуни, например: Бр.АЖ9-4, ЛМЦ С58-2-2 и д.р.

3. при скоростях скольжения V <2м/сек. – серый чугун (СЧ 15-32;СЧ 18-36;СЧ 24-44)

Червяки, как правило, изготовляются из стали. С увеличением твердости и чистоты рабочих поверхностей витков червяка уменьшается возможность заедания передачи. (намазывания бронзы на червяк). Поэтому, высокая твердость рабочих поверхностей в сочетании с высокой чистотой обработки является одним из основных потребностей при изготовлении червяков.

Геометрия.

Червяки в червячных передачах применяется цилиндрические и глобоидные.

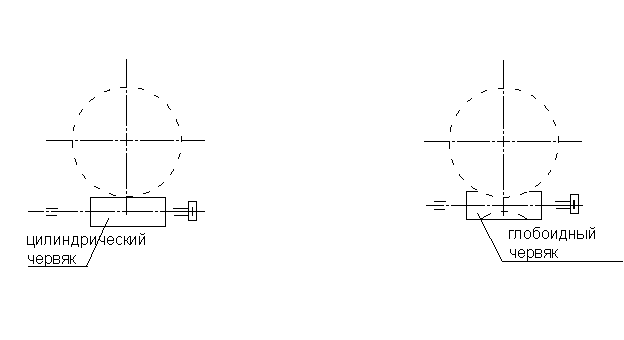
Здесь мы ознакомимся с геометрии передачи с цилиндрическим червяком.

Образование поверхности витков цилиндрического червяка можно представить себе также, как и образование винта. Если в осевом сечении червяка боковые поверхности витков пересекаются по прямым линиям, то такие червяки называются архимедовыми. Применяются так же червяки, боковые поверхности витков в осевом сечении очерчены по Эвольвентам. У архимедовых червяков угол “Х” делаются равным 20 . Таким образом, угол при вершине профиля 2х=40 .

Введем следующие обозначения:

Z - число заходов червяка. Стандартами(ГОСТ 2144-76) установлены значения Z =1,2 и 4.

Z - число зубьев червячного колеса.

Р- осевой шаг червяка или торцевой шаг червячного колеса.

m= осевой модуль червяка или торцевой модуль червячного колеса.

q= - коэффициент диаметра червяка, где d -диаметр делительной окружности червяка.

-угол подчала витка червяка по делительному цилиндру.

Для определения угла развернем один виток червяка на плоскость.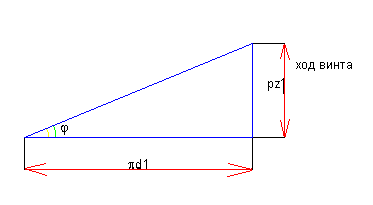

Ниже приведем формулы для определения основных параметров червячной передачи при X =0:

d =mq – диаметр делительной окружности червяка

d =mz -диаметр делительной окружности червячного колеса.

- межосевое расстояние,

d =d+2m-диаметр окружности вершин витков (зубьев) червяка (колеса),

d =d-2,4m – диаметр окружности впадин витков (зубьев) червяка (колес),

- угол подъема витка червяка по делительному цилиндру,

2 -угол обхвата червяка колесом,

sin

В ширине червячного колеса.

b= 0,75 d - при Z =1,2

b=0,67 d -при Z =4.

Вопросы для самоподготовки:

1. Какова взаимосвязь между силами, приложенными к шестерне и колесу конической передачи?

2. Как поменять действие окружных составляющих на противоположное?

3. Понятие о “эквивалентной цилиндрической передаче” при расчетах конических передач.

4. Что скрывается за понятием “одинаковая нагрузочная способность” конической и эквивалентной ей цилиндрической передачи?

5. Особенности расчета конических передач на изгиб.

6. Как учитывается пониженная нагрузочная способность конических передач по сравнению с цилиндрическими?

7. Какой модуль определяется при проектировочном расчете конических передач на изгиб?

8. Достоинства и недостатки червячных передач.

9. Материалы червяков и червячных колес.

10. Какие формы червяков Вы знаете?

11. Что такое число заходов червяка?

12. Что такое коэффициент диаметра червяка?

ЛЕКЦИЯ №10

Кинематика червячной передачи (0,25 часа).

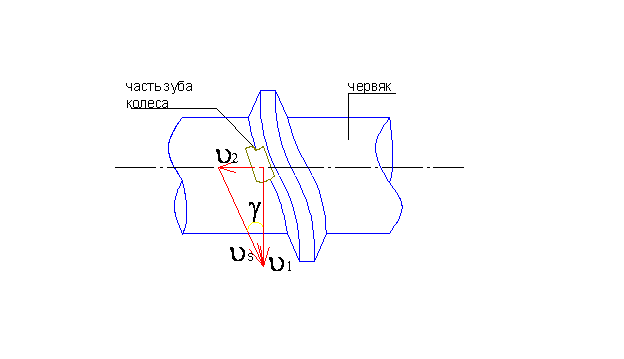
1.Скорость скольжения υs

При работе передачи витки червяка скользят по зубьям колеса, как в винтовой паре. При этом скорость скольжения направлены по касательной к винтовой линии червяка. Как относительная скорость червяка и колеса, которые в данном случае являются окружными скоростями

2)Передаточное число.

Передаточное число червячной передачи определяется по формуле:

Имея в виду, что:

d

получаем:

Силы, действующие в зацеплении (0,25 часа).

В червячном зацеплении действуют:

-окружающая сила на червяке, равная осевой силе на колесе:

F

-окружная сила на червячном колесе, равная осевой силе на червяке:

-радикальная сила на червяке и черв. Колесе:

Сила Fn здесь является нормально к профилю витка червяка только в осевом его сечении. Нормальная сила Fn, перпендикулярная к поверхностям контакта витков червяка и зубьев червячного колеса, определяется по формуле:

Зависимости между моментами на червяке и колесе имеет вид:

Т =Т , где: - к.п.д. червячной передачи.

Расчетная нагрузка (0,5 часа).

Расчетная погонная нагрузка «q » в случае червячной передачи определяются по формуле:

q где: (а)

К – коэффициент нагрузки представляющий собой произведение двух коэффициентов:

К=К где:

К -коэффициент неравномерности распределения нагрузки по длине контакта,

К -коэффициент динамичности нагрузки.

Коэффициент неравномерности распределения нагрузки К можно определить по формуле:

К , где:

-коэффициент деформации червяка, зависающий от параметров червяка Z и q.

X- отношение среднего повременного момента к максимальному:

X=

При постоянной нагрузке К

Коэффициент динамичности нагрузки К выбирается в зависимости от величины окружной скорости червячного колеса . При принимают К . При значение К принимают как для цилиндрических косозубых передач с твердостью рабочих поверхностей зубьев HB и той же степени точности.

Для предварительных расчетов коэффициента нагрузки можно принять: К=К

Суммарная длинна контактных линий в случае червячной передач определяется по аналогии с косозубой цилиндрической передачей, для которой она определялась по формуле:

.

В случае червячной передачи вместо ширины колеса «b» берется длинна дуги делительной окружности червяка в пределах условного угла обхвата червяка колесом 2б. Длинна этой дуги будет очевидно равно:

Вместо угла наклона зуба в плоскости зацепления в случае червячной передачи берется угол подъема витка червяка по делительному цилиндру .

Коэффициент колебаний суммарной длинны контактных линий для червячной передачи берется К .

Тогда, суммарная длинна контактных линий для червячной передачи определиться по формуле:

.

Приближение можно принять:

2

Тогда:

Подставляя теперь формулу (а):

Fn=

Коническую погонную нагрузку получаем в следующем виде:

q

Принимая , окончательно получаем:

q

Расчет на контактную прочность (0,75 часа).

Расчет червячной передачи на контактную прочность предусматривает предупреждение разрушения передачи как вследствие заедания, так и вследствие выкрашивания рабочих поверхностей зубьев. Известно, что оба эти виды разрушения являются результатом возникновения в зацеплении больших контактных напряжений сжатия.

Поэтому, условие прочности червячной передачи по контактным напряжениям сжатия может быть записана также формулой Герца.

(1)

Расчетная погонная нагрузка «q » для подставки в эту формулу нами найдена выше.

Найдем теперь приведенный радиус кривизны контакта « ». Приведенный радиус кривизны контакта должен быть найден в сечении, перпендикулярным к виткам червяка и зубьям червячного колеса. В случае архимедового червяка в осевом его сечении червяк и червячное колесо дают зацепление косозубого колеса с рейкой (так как в этом сечении боковые стороны витков червяка – прямые линии).

Правда, в сечении, перпендикулярном к виткам червяка, боковые их стороны очерчиваются по линиям, несколько отличным от прямой, но все же их радиус кривизны достаточно велик, т.е. S . Поэтому проведенный радиус кривизны контакта витка червяка и зуба червячного колеса определяется только радиусом кривизны боковой поверхности зуба колеса:

= =

По аналогии с косозубым колесом радиус кривизны боковой поверхности зуба червячного колеса (а, следовательно, и приведенный радиус кривизны контакта) определяется по формуле:

Теперь в формулу (1) подставляем:

; ; (для стали, чугуна, бронзы); (модуль упругости стального червяка); (модуль упругости бронзового или чугунного венца червячного колеса). При этом приведённый модуль упругости для такой пары материалов будет: = .

В результате получаем формулы для проверочного и проектного расчётов червячной передачи по контактным напряжениям в следующем виде:

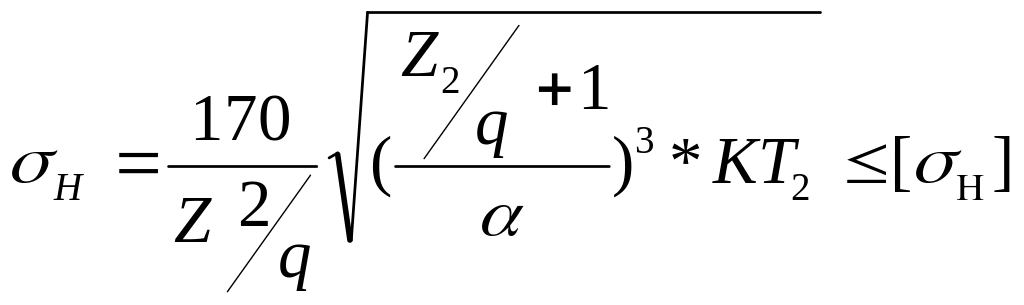(2)

(3)

В формулах (2) и (3):

мм

Н *мм

и [ ] -

В червячных передачах для параметров Z и q существует следующее рекомендуемое соотношение:

Если при выборе Z и q придерживаться этой рекомендации, формулы для проверочного и проектного расчетов червячной передачи можно написать значительно проще:

(4)

мм (5)

Допускаемые контактные напряжения ( 0,25 часа).

Величина допускаемого контактного напряжения зависит, главным образом, от материала венца червячного колеса. Выше было сказано, что материалы, применяемые для червячных колес, могут быть условно сведены в три группы.

1. В случае применения для червячных колес оловянистых бронз, допускаемое контактное напряжение определяется по формуле:

где:

- предел прочности материала венца, ;

С - коэффициент, принимаемый в зависимости от скорости скольжения (в таблицах);

N

При постоянной нагрузке число циклов нагружения зубьев червячного колеса равно:

N

2. В случае применения для червячных колес безоловянистых бронз и латуни допускаемые контактные напряжения определяются по формуле:

где:

- скорость скольжения в

3. В случае применения для червячных колес серого чугуна допускаемые контактные напряжения определяются по формуле:

Вопросы для самоподготовки:

1. Что такое скорость скольжения в червячной передаче?

2. Как записывается передаточное число для червячной передачи?

3. Какова взаимосвязь между силами, приложенными к червяку и червячному колесу?

4. Как оценивается коэффициент нагрузки в червячной передаче?

5. Как определяется минимальная суммарная длина контактных линий в червячной передаче?

6. Как оценивается расчетная нагрузка в червячной передаче?

7. Особенности оценки приведенного радиуса кривизны в червячной передаче?

8. Особенности оценки приведенного модуля упругости в червячной передаче?

9. Каким образом можно упростить формулы при расчете на контактную прочность червячной передачи?

10. В зависимости от чего определяются допускаемые напряжения на контактную прочность в червячных передачах?