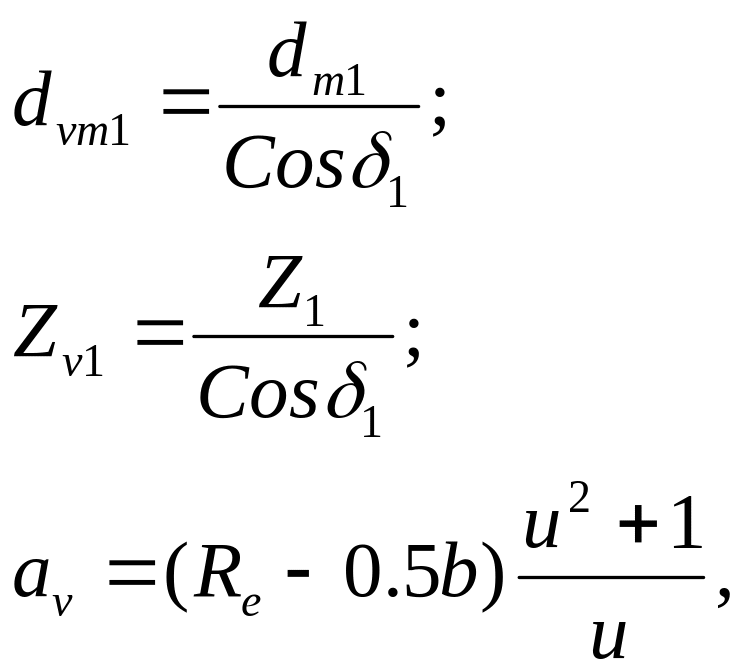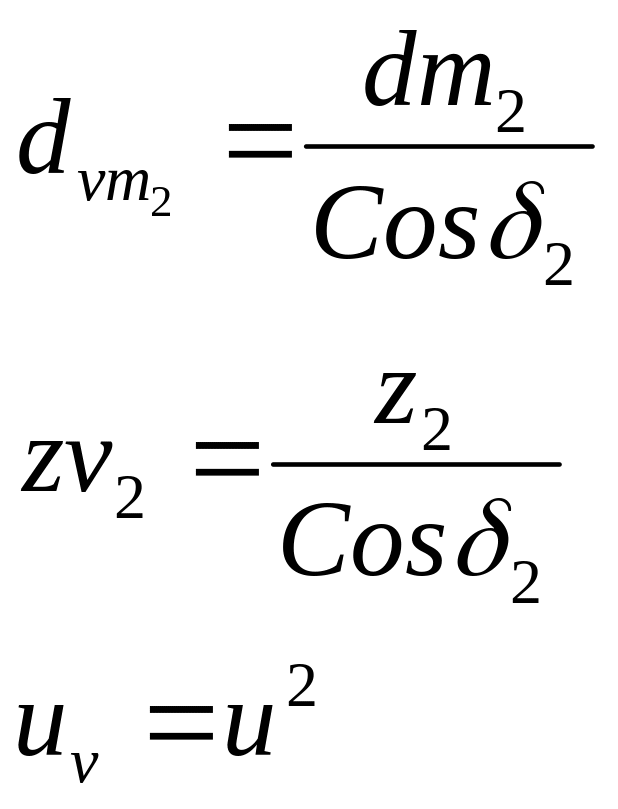Лекция № 8

Принципиальные положения расчета косозубых передач на прочность (как по контактным, так и по изгибным напряжениям) аналогичны приведенным в расчете прямозубых передач. В случае косозубых передач нами будут рассмотрены лишь некоторые особенности расчета, обусловленные геометрией косозубых передач (например, больший коэффициент перекрытия, наклонное положение контактной линии на боковой поверхности косого зуба и т.д.)

Силы, действующие в зацеплении (0,5 часа).

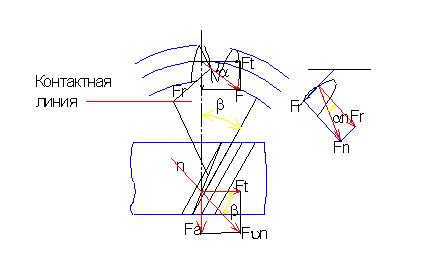
Силы, действующие в зацеплении косозубой передачи нами, будут рассмотрены без учета сил трения. Причем, в случае косозубой передачи эти силы удобно представить в виде параллелепипеда.

Если не учитывать трения, сила полного давления на зуб F_n действует в плоскости зацепления нормально к поверхностям зубьев. Эту нормальную силу можно разложить на три взаимно перпендикулярные составляющие:

Окружную силу F_t,

радиальную силу F_r,

и осевую силу F_a.

При определении сил, действующих в зацеплении, будем исходить из момента на колесе T₂, считая его известным. При этом отдельные составляющие нормальной силы на зуб будут равны:

Направления окружного и радиального усилий будут такие же, как и в случае прямозубой передачи.

Направление же осевого усилия F_a зависит от направления вращения и наклона зубьев. Для одной и той же пары косозубых колёс при изменении направления вращения направление осевого усилия меняется на противоположное.

Определим нормальную силу F_n:

Учитывая, что , имеем:

По силам F_t, F_r и F_a обычно ведутся расчеты валов и подшипников, а расчет самого зубчатого зацепления на прочность ведётся по силе полного давления F_n.

Особенности расчета косозубых цилиндрических передач на прочность (1 час).

а) Расчет на контактную прочность.

При выводе расчетной формулы для косозубых передач на контактную прочность исходная формула, представляющая собой условие прочности передачи по контактным напряжениям, записывается также, как и для прямозубых передач:

(1)

При расчете косозубых цилиндрических передач контактную прочность следует учесть следующие особенности этих передач:

1)Косозубые передачи проектируются таким образом, чтобы в зацеплении постоянно находились бы не менее двух пар зубьев. Так как косозубые колёса относительно хорошо прирабатываются, в расчетах предполагают, что нагрузка воспринимается всеми зубьями, находящимися в зацеплении. Поэтому, в случае косозубой передачи длина контакта между колёсами принимается равный не размеру ,,b”, а значительно больше. Появляется понятие суммарная длинна контактных линий , величина в принципе переменная.

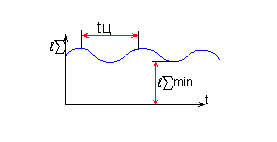
Причем, период колебании этой величины равен времени поворота колеса на один торцевой шаг. Нас, естественно, интересует минимальное значение , когда погонная нагрузка по

длине контакта будет максимальной. Минимальная суммарная длина контактных линий определяется по формуле:

, где:

b- ширина передачи,

торцевой коэффициент перекрытия,

- коэффициент колебаний суммарной длины контактных линий. В косозубых передачах можно принять =0,9...0,95, а в шевронных =0,95...0,98.

- угол наклона зубьев на основном цилиндре, где:

Поэтому расчетная нагрузка ,,q” для подстановки в формулу (1) в случае косозубых передач должна определятся по формуле:

2)Приведенный радиус кривизны ,, ” для подстановки в формулу (1) в случае косозубых передач должен определятся в сечении, перпендикулярном к контактной линии. В этом сечении радиус кривизны профиля зуба равен

(теорема Менье):

, где:

- радиус кривизны профиля в торцевом сечении, равный:

Тогда радиусы кривизны профилей зубьев шестерни и колеса в сечении, перпендикулярном к контактной линии, будут:

И, наконец, приведённый радиус кривизны контакта:

С учётом приведенных выше особенностей расчета косозубых цилиндрических переда формулы для проверочного расчётов по контактным напряжениям напишем без вывода в контактом виде:

(2)

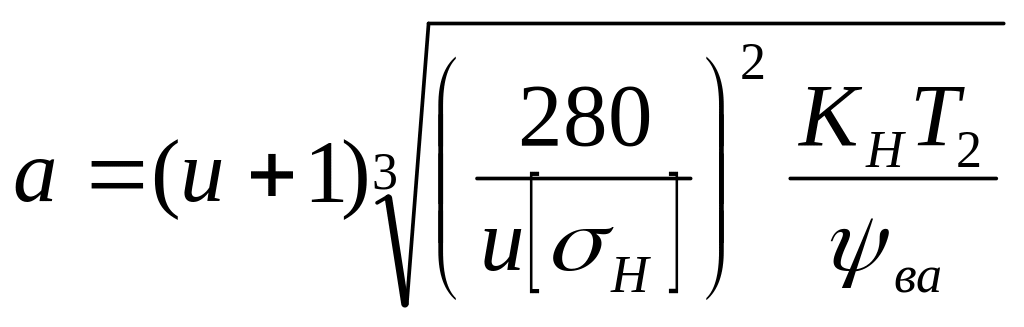мм (3)

В формулах (2) и (3):

а и b – в мм

Т₂ – в Н*мм

- в

Определение коэффициента нагрузки К_H и допускаемого напряжения осуществляется точно также, как и в случае прямозубых передач.

При проверочном расчете по формуле (2) допускается превышение сверх до 5%. При большей разнице требуется пересчет межосевого расстояния по формуле (3).

б) Расчет зубьев на изгиб.

При выводе расчетных формул для расчета косозубых передач по изгибным направлениям в зубьях следует учесть, что косые зубья значительно прочнее прямых. Объяснить это можно следующими причинами:

1. Участие в зацеплении нескольких пар зубьев, учитываемое коэффициентом 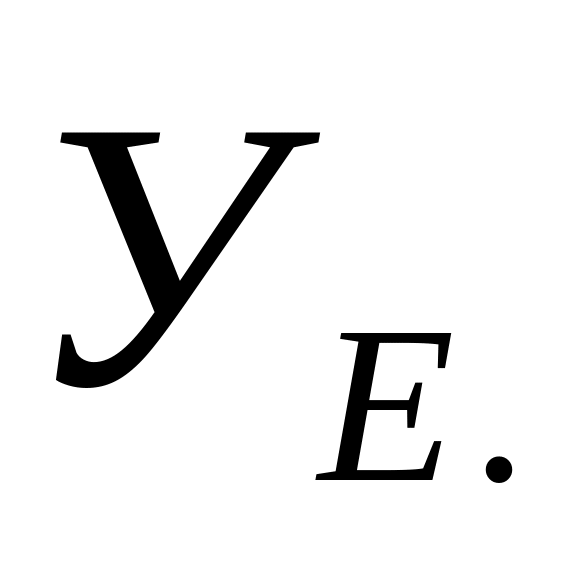Коэффициент У_Е можно принять: У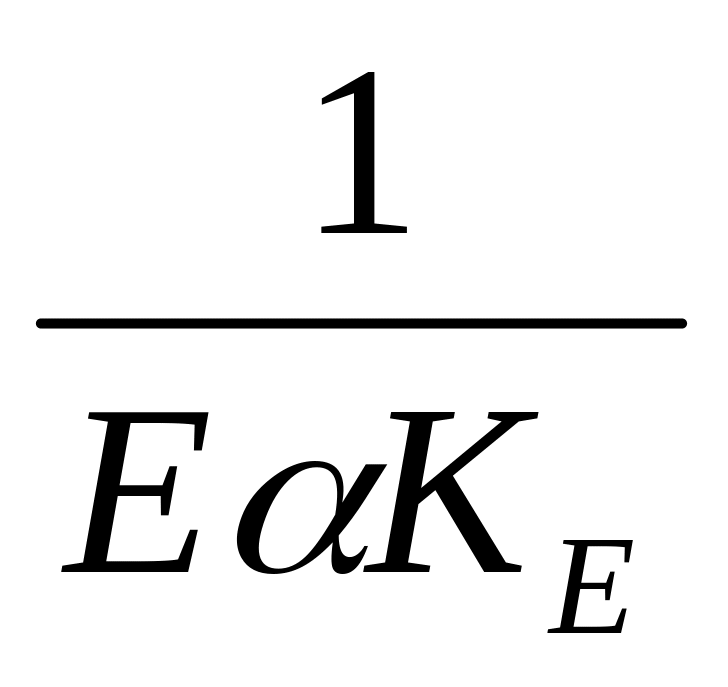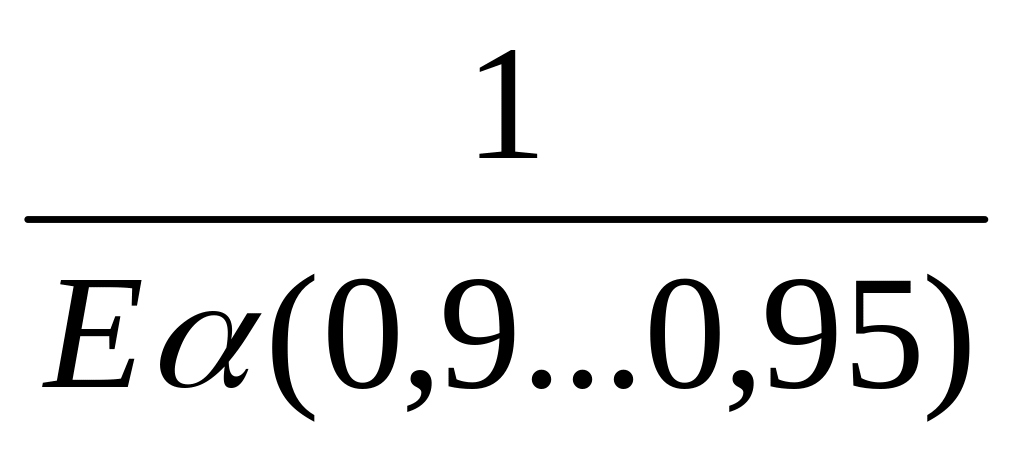_Е = = , где Е - торцевой коэффициент перекрытия, который с достаточной точностью может быть определен по формуле: Е = 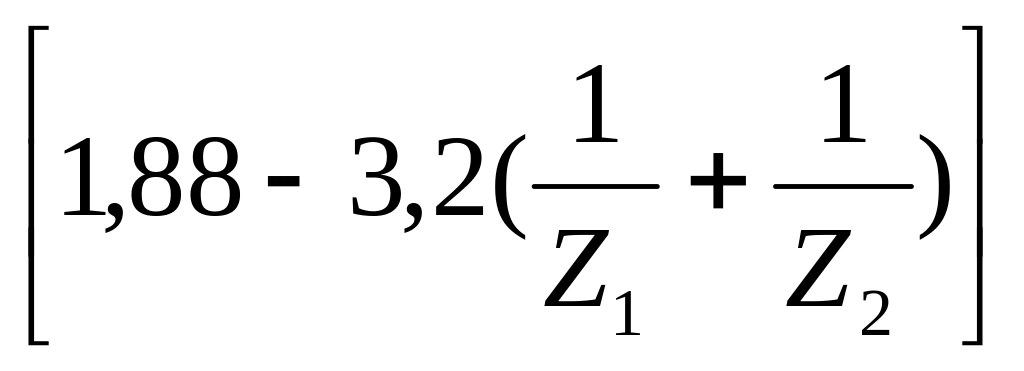Cosβ.

Здесь Z₁ и Z₂ – числа зубьев шестерки и колеса.

2. Контактная линия на боковой поверхности косого зуба занимает наклонное положение.

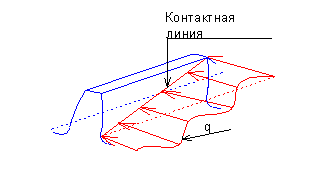
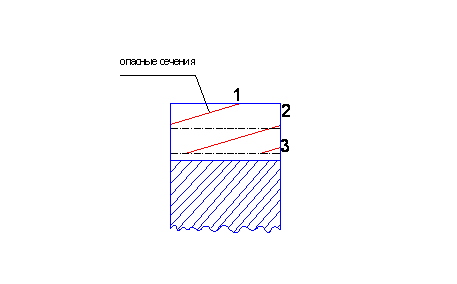
По линии контакта нагрузка распределяется непрерывно. Она имеет максимум на средней линии зуба, так как в момент зацепления серединами суммарная жесткость пары зубьев тоже имеет максимальное значение.

Направления в опасном сечении косого зуба вызывается только той частью нагрузки, которая лежит выше опасного сечения. Дело в том, что в процессе зацепления пары косых зубьев контактная линия попеременно занимает положения 1, 2, 3 и само опасное сечение оказывается наклонным. При этом опасным может оказаться положение 1, при котором у зуба отламывается угол. Ясно, что на участке контактной линии 1 передается небольшая часть нагрузки и в опасном сечении косого зуба изгибные направления должны быть меньше, чем в опасном сечении прямого зуба.

Некоторые уменьшения изгибных напряжений в опасном сечении косого зуба в связи с вышесказанным учитывается коэффициентом Y . На основе экспериментальных данных:

3. Коэффициент формы зуба Y_F в случае косозубых передач выбираются в зависимости от эквивалентного числа зубьев 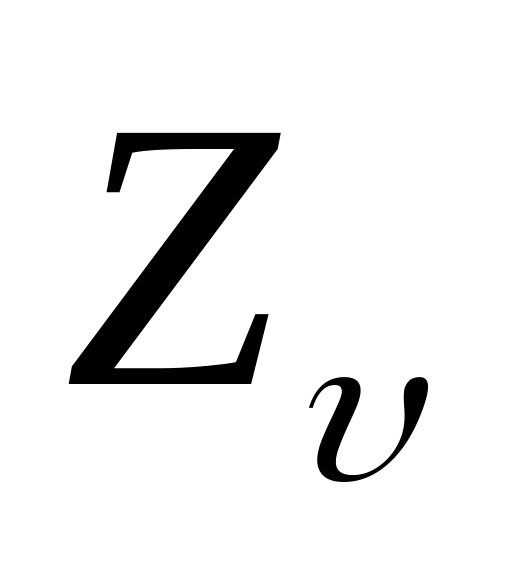,равного:

, где:

Z – фактическое число зубьев

Таким образом для косозубой передачи при равных числах зубьев коэффициент формы зуба Y_F будет меньше.

С учетом перечисленных особенностей косозубых передач, не останавливаясь здесь на выводе, итоговые формулы приведенного и проектного расчетов по изгибным напряжениям можно представить в следующем виде:

(4)

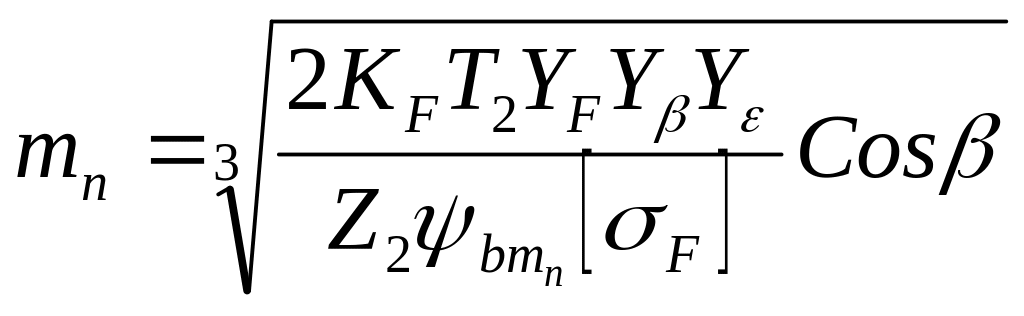мм (5)

В формулах (4) и (5):

b и m_n – в мм

T₂ – в

(при проектировочном расчете по формуле (5) задаемся сами)

Определение коэффициента нагрузки K_F и допускаемого напряжения осуществляется точно также, как и в случае прямозубых передач.

Некоторые особенности расчета по формулам (4) и (5) в зависимости от материалов шестерни и колеса остаются такими же, какие они были для прямозубых передач.

Заканчивая рассмотрение косозубых цилиндрических передач, следует сказать несколько слов о рекомендуемых значениях угла наклона зубьев ,,β”.

При назначении угла наклона зубьев,,β” нужно помнить, что косозубые колеса стоят несколько дороже, чем прямозубые. Поэтому назначить слишком малый угол β нет смысла, так как при этом удорожание производства не окупается мизерным увеличением коэффициента перекрытия передачи. С другой стороны, большие β вызывают большие осевые усилия F_a, что, в свою очередь, может вызывать необходимость постановки в опорных узлах упорных подшипников и усложнить конструкцию опор.

С учетом всего сказанного, обычно, угол наклона косых зубьев принимают β= .

Расчет шевронных передач как на контактную прочность, так и на изгиб зубьев совершенно аналогичен косозубым. Шевронные колеса делают с углом наклона зубьев до и более. В данном случае осевые силы на полу шевронах взаимно уравновешиваются. Если учесть, что шевронные передачи и по ширине делаются значительно шире, чем просто косозубые, можно себе представить насколько больше получается, коэффициент перекрытия в этих передачах и насколько плавно они работают.

Особенности расчета закрытых и открытых косозубых и шевронных передач те же, что и в случае прямозубых цилиндрических передач, а именно а) при расчете закрытых передач основным расчетом является расчет по контактным напряжениям, а расчет зубьев на изгиб является только проверочным.

б) при расчете открытых передач основным и единственным расчетом является расчет зубьев на изгиб.

Конические зубчатые передачи.

Геометрия (0,5 часа)

Конические зубчатые пары применяются в передачах между валами, оси которых пересекаются под некоторым углом. Межосевой угол может изменяться в широком диапазоне значений (он может быть и острым и тупым) но наибольшее распространение получили передачи с , называемые ортогональными.

Конические зубчатые колеса выполняются с прямыми, косыми и криволинейными (круговыми) зубьями. Здесь мы ознакомимся с геометрией прямозубой конической передачи с углом

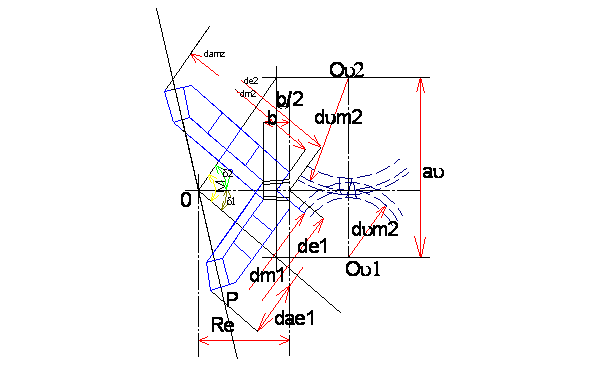
Конусы SOQ и QOP при вращении колес катятся друг по другу без скольжения и называются начальными конусами. Следует отметить что в конических зубчатых передачах начальные конуса, как правило, совпадают с делительными конусами, так как конические зубчатые передачи обычно выполняются с .

Обозначим:

и -диаметры внешних делительных окружностей,

и - диаметры внешних окружностей по вершинам зубьев,

d_m1 и d_m – диаметры внешних делительных окружностей,

b – ширина зубчатого венца,

R_e – конусное расстояние,

δ₁ и δ₂ – углы делительных конусов.

Если , то:

где:

u – передаточное число.

Условимся, обозначать:

m_te – модуль на внешней делительной окружности,

m_tm – модуль на средней делительной окружности.

Тогда основные размеры конической передачи могут быть записаны формулами:

Если обозначить:

,

то параметры на средней делительной окружности, записанные через соответствующие параметры на внешней делительной окружности, будут:

d_m=(1-0.5K_be)d_e;

m_tm=(1-0.5K_be)m_te.

Для упрощения прочностных расчетов обычно коническую передачу заменяют эквивалентной ей цилиндрической передачей с размерами зубьев, равными размерам зубьев конической передачи в среднем сечении. Принцип образования эквивалентной цилиндрической передачи показал на рисунке. Основные параметры эквивалентной цилиндрической передачи показал на рисунке. Основные параметры эквивалентной цилиндрической передачи определяются через соответствующие параметры конической передачи следующим образом: