Косозубые цилиндрические передачи

Геометрия (0,5 часа).

Зубчатые колеса с косыми зубьями применяются для увеличения коэффициента торцевого перекрытия передачи. Это видно из следующей формулы:

, где:

- коэффициент перекрытия для косозубой передачи,

- коэффициент перекрытия для аналогичной по размерам (в торцевом сечении) и числам зубьев прямозубой передачи.

b- ширина передачи

P_t- шаг зацепления в торцевом сечении

- угол наклона зубьев.

Известно, что в прямозубых передачах коэффициент перекрытия делается больше единицы, т.е. и в прямозубых передачах в среднем в зацеплении находится больше одной пары зубьев.

Известно, что и в прямозубых передачах коэффициент перекрытия делается больше единицы, т.е. и в прямозубых передачах в среднем в зацеплении находится больше одной пары зубьев. Однако неизбежные погрешности при изготовлении колес(непостоянство шага, отклонения от профиля и т.д.) приводят к тому, что теоретическое значение коэффициента перекрытия в действительности не реализуется. Число пар зубьев, находящихся в зацеплении в действительности, оказывается меньше. Это проявляется в работе передачи с ударами и шумом, причем, тем в большей степени, чем больше окружная скорость в зацеплении. Увеличение коэффициента трения в косозубых передачах в сравнении с прямозубыми с этой точки зрения является весьма полезным фактом. Обычно, применение прямозубых передач считается возможным при окружных скоростях ν≤ . При окружных скоростях в зацеплении ν>3 рекомендуется применять косозубые передачи. Этим обеспечивается плавность работы передач.

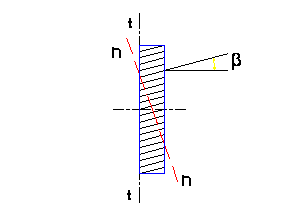
Основные размеры косозубых колес определяются по тем же формулам, что и в случае прямозубых колёс, подставляя в некоторые из них значения модуля в торцевом сечении t-t, в некоторые значения модуля в нормальном к зубьям сечении n-n.

Здесь мы приведем некоторые формулы для определения основных параметров колес и передачи в целом, справедливые для передач с .

Принято обозначать:

m_t- модуль в торцевом сечении t-t

m_n- модуль в нормальном сечении n-n

Z- число зубьев.

Тогда:

1. d=m_t*Z- диаметр делительной окружности.

2. d_a=d+2m_n+2x_nm_n-диаметр окружности вершин.

3. d_f=d-2m_n+2x_nm_n- диаметр окружности впадин.

4. a=

Причем, между торцевым модулем m_t и нормальным модулем m_n существует зависимость:

Нормальный модуль m_n делается стандартным.

В косозубых передачах в нормальном к зубьям сечении угол зацепления α_n делается равным . Угол зацепления в торцевом сечении α можно найти по формуле:

Тогда диаметр основной окружности косозубого колеса может быть определен по формуле:

5)

Вопросы для самоподготовки

1. Как выбирается базовый предел выносливости материала колес по изгибным напряжениям для пульсирующего цикла?

2. В зависимости от чего назначается коэффициент безопасности при расчете допускаемых напряжений на изгиб?

3. Как определяется коэффициент реверсивности?

4. От чего зависит вид формулы для оценки коэффициента долговечности?

5. Для каких передач расчет на изгиб является основным проектировочным?

6. Для каких передач расчет на изгиб является проверочным?

7. Методика проверочного расчета на изгиб цилиндрических прямозубых передач.

8. В чем основные преимущества косозубых цилиндрических передач по сравнению с прямозубыми?

9. В чем проявляются недостатки косозубых цилиндрических передач по сравнению с прямозубыми?

10. В каких сечениях рассматриваются геометрические размеры колес косозубой цилиндрической передачи?

11. Какой модуль гостируется в косозубой цилиндрической передаче?