1.Предмет ТВ.ТВ-это раздел матем.,изуч.в абстрактной мат.форме закономерности реальных массовых случайных явлений.К развитию ТВ в 17в. Привели след.задачи:1)расчет вер-ти выйгрыша в азартных играх2)задачи страхования3)задачи демографии4)задачи теории стрельбы5)задачи теории наблюдения.Основоположники:П.Рерша и Б.Паскаль.Русская школа:Буняковский(автор первого курса тв на русском языкеи создатель соврем. термин-и)Чебышев(закон больших чисел)Марков(основы случайных процессов)Ляпунов.Соврем.этап:Слуцкий,Смирнов,Хинчин,Ромашевский.

2.Случайные события и их классификация.

Событие-это первонач.понятие которое поясняется.Изучение любого события связано с осуществлением некотрого комплекса условий-опыт.События:1)достоверные(обяз.произойдут)невозможные(никогда не произойдут)случайные(или произойдут или нет)2)элементарные и разложимые3)несовместные(А1 А2…Аn –несовм.если появление одного исключает появление другого)совместные.События ед.возможные и несовместн.-полная группа событий.2 ед.возможн. и несовсм.события-противоположные.

3.Классическое,статистическ.,геом.,аксиометр. Определение вер-ти.а)класс.:все элементы события в данном опыте равновозможны,тогда вероятн.соб А называется число,обознач. Р(А)=m/n,где m-число исходов,благоприятствующих появл.соб.А,n-исходы,ед.возможные,равновозм.и несовместн.Свойства:1)Р(Ω)=1 (m( Ω)=n,P(Ω) =n/n=1) 2)Р(невозм.соб.)=0 Док.:m(невозмо)=0,P=(невозм.)=0/n=0 3)0<p(a)<1 (0<m<n,O/n<m/n<n/n, 0<Р(А)<1). б)статист.:пусть некот.опыт повторен n и в результате событие А наступило m раз.Дробь w(А)=m/n называется относ.частотой. события А.Если отн.частота обладает устойчиостьюи при неогр.кол. n и все относ частоты группируются возле числа Р*,то это число называется стат.вер-ю соб А. в)геометр.:найти вероятность что точка будет внутри круга.Р=Sкр /Sкв. г)аксиом.:вероятность определяется через систему аксиом.

4.Алгебра событий.Суммой соб. А и В назыв. Соб. Обозначаемы А+В, состоящие в том,что происходит хотя бы одно из тех соб: или А, или В, или А и В вместе.Произведение соб. А и В назыв. Соб. АВ, состоящие в том,что происходят и соб. А и соб.В, т.е. оба соб вместе. Соб.А содержится в соб В или А влечёт В (А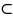 В), если всякий раз,когда происходят соб.А происходит и соб В.Если А В и В , то соб.-равные. Св-ва: А+В=В+А 2)АВ=ВА 3)А+ =Ω 4) =А

5.Элем-ты комбинатор:размещ,перестан и сочет.Св-ва сочет.Размещ. с повтор.Комбин-раздел матем, кот. Изучает способы упорядочения конечной совокупности объектов.В Правила:1) пр.Суммы.Если объект А можно выбрать m способами, а др. объект В можно выбрать n способ,то выбрать А или В можно m+n способ. 2) пр. произведения. Если объект А можно выбрать m способ и после каждого такого выбора объект В можно выбрать n способ,то пару(А,В) в указанном порядке можно выбрать mn способ. А)РАЗМЕЩЕНИЕ:пусть имеется конечное n-элементное множество.Любое его к-элемент. Упорядоченное подмнож. назыв. размещением из n элем. по к элем.Число размещ. обозначается А n(n-1)…(n-k+1) Или А = Б)ПЕРЕСТАНОВКА: переест. из данного n-элемент. множеств назыв. размещение по n элемент. В)СОЧЕТАНИЕ: соч. из n элем. по к элем. назыв. всевозможные неупорядоченные к-элемент. подмножества данного n-элемен. множества.Число соч. обознач. С = . Соч. используется там,где порядок следования элем. не играет роль.Св-ва: 1) С 2) C 3)C =n.Г)РАЗМЕЩЕНИЕ С ПОВТОР:если выбор к-элем. подмножества из n-элем. множества происходит с возвращением отобранного элем. в исходное и упорядоч. отобранных элем.в последов.цепочку, то полученные подмножества назыв.размещ.с повтор. .

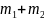6.Теорема слож. вероят.несовместных соб и её следств.Теорема:Вероятность Р(А+В)=Р(А)+Р(В).Доказат: пусть соб.А благоприят. исходов из n исходов,а В благоприят. исходов из n исходов.Так как А и В несовместны, общих исходов нет.Значит А+В благоприят.( ) исходов из n. Р(А+В)= = + =P(A)+P(B). Следствие1:данная теорема справедлива и для Р( )=P(A)+P( )+…+P( ) След2:если соб. Образуют полную группу , то сумма их вероятностей равна 1. Р(А1)+Р(А2)+…+Р(Аn)=1. След3:Сумма вероятн противоположных соб равна 1.Р(А)+Р( )=1.Принято Р(А)=р, Р( )=q.

7.Завис. и независ-е события.Условная вер-ть.Т.умнож.вер-тей.

Условной вер-тью соб-я В наз-ся вер-ть события В вычисл-ое при условии А, что событие произошло и обознач. Р(В/А)= (В).

Т.умнож.завис.событий:Р(АВ)=Р(А)*Р(В/А)

(позвол.решать задачи для 3 соб-ий: (Р(АВС)=Р(А)*Р(В/А)*Р(С/(АВ)) )

Говорят,что соб.В не зависит от соб.А,если Р(В/А)=Р(В).Это рав-во служит мат.критерием нзав-ти двух событий.Если оно вып-ся,то соб.А и В независимы.

Т.умнож.независ.событий:Р(АВ)=Р(А)*Р(В). Можно показать,что если соб.АиВ нез-мы,то незав-ми явл.след.пары собитий ВиА: А иВ,В иА,А и В, А иВ, А и В. Несколько событий являются незаис. в совокуп-ти,если они попарно независ.и каждое соб.независио от любо комбин.В это случ.Т.умн.запис-ся в виде:Р( )=Р( Р( …Р( ).

8.Вер-ть появл-я хотя бы одного из n соб-ий,независ.в совокуп-ти.Вер-ть того,что хотя бы 1 из n соб.незав.в сов-ти произойдет равна разности между единицей и проивед.вер-ти протиопол.событий:Р( )=1- . Док-во: события( )и ( ) явл-ся противоположными.Значит сумма их вер-тей равна 1.Р( )+ ( )=1.Тогда применяется Т.умн.В итоге: Р( )= 1- . Следствие:если Р( ,то

9.Т.слож.вер-тей совместных событий.Вер-ть наступл-я только 1, хотя бы 1 события. Р(А+В)=Р(А)+Р(В)-Р(АВ) (в свою очередь Р(АВ)Р(А)Р(В) или Р(А)Р(В/А))-если события совместны.

А+В=АВ+АВ+АВ, тогда Р(А+В)=Р(АВ)+Р(АВ)+Р(АВ)*-если несовместны. С др.стороны соб.А=АВ+АВ, Р(А)=Р(АВ)+Р(АВ)Р(АВ)=Р(А)-Р(АВ)**

В=АВ+АВ, Р(В)=Р(АВ)+Р(АВ), Р(АВ)=Р(В)-Р(АВ)***. Подставляем ** и *** в * и получим Р(А+В)=Р(А)+Р(В)-Р(АВ).

Хотя бы 1: ; Только 1: .

10.Формула полной вероятности и формулы Байеса.Теорема. Если событие А может произойти лишь при условии наступления 1-го из n независимых событий гипотез Н₁,Н₂…Н_n, образующих полную группу(Р(Н₁)+Р(Н₂)+…+Р(Н_n)=1),то полная вер-ть события А рассчитывается по формуле:

Р(А)=Р(Н₁)*Р(А/ Н₁)+ Р(Н₂)*Р(А/ Н₂)+…+ Р(Н_n)*Р(А/ Н_n)=

Условные вер-ти гипотез, вычисляемые при условии, что событие А произошло называется послеопытными вероятностями, вычисляются по формулам Байеса:

Р(Н₁ /А) =

Док-во: Поскольку событие А зависит от Н₁, то и Н₁ зависит от А, тогда применяя теорему умножения вероятностей зависимых событий к левой и правой части равенства АН₁ = Н₁А, получаем Р(АН₁)=Р(Н₁/А), Р(А)*Р(Н₁/А)=Р(Н₁)*Р(А/Н₁), но Р(А)≠ 0.

Р(Н₁/А)=