10.1. Передаточная функция разомкнутого контура регулирования.

Эту передаточную функцию W(p) необходимо представить и в общем виде (1), и в виде (2) с числами (обязательно и так, и так; это необходимо для удобства проверки):

W(p) = W₁(p) W₂(p) W₃(p) = k₁k₂k₃ ; (1)

W(p) = . (2)

K = k₁k₂k₃ = 14,0 3,00 1,00 = 42,0 – коэффициент передачи разомкнутого контура регулирования ("добротность системы").

Никаких дополнительных требований для этой ПФ нет.

10.2. Передаточная функция замкнутой системы.

 (p) =

W_П(p) = W₁(p)W₂(p) – ПФ прямой цепи контура.

Знаменатель  (p): p³ + 7,17p² + 59,4p + 140 (с единицей при p³).

Корни знаменателя: p₁ = – 2,99; p₂ = – 2,09 – 6,52j; p₃ = – 2,09 + 6,52j.

Таким образом, ПФ замкнутой системы:

 (p) = , (3)

где К_ЗАМ  1 мм/В – коэффициент передачи замкнутой системы; это соотношение будет справедливо, если корни знаменателя определены правильно и выдержана необходимая точность. Если это так (см. методичку [М1]), то в дальнейшем можно всегда считать, что К_ЗАМ ≡ 1.

ПФ  (p) необходимо представить в виде (3), причем в скобке звена второго порядка знаменателя должны быть выделены постоянная времени Т и параметр затухания  (в данном случае запись должна быть такой: Т²p²+ 2Tp + 1 = (0,146)²p² + 20,3050,146p + 1, где Т = 0,146 с;  = 0,305);

Это тоже необходимо для удобства проверки всего ДЗ.

10.3. Передаточная функция замкнутой системы по ошибке.

_(p) = = , (4)

Коэффициент передачи замкнутой системы по ошибке: К_ = = = 0,0238 с.

Передаточная функция _(p) должна быть представлена в виде (4).

11) Количество разрядов при вычислении и записи величин.

Все вычисления будем выполнять с одним числом значащих цифр и в исходных данных, и в результате операции. Для некоторых чисел будут «лишние» разряды, но недостаточной точность не будет никогда.

Рассмотрим результат вычисления, который представлен ранее, в предыдущем пункте: К_ = 0,0238 с. Этот результат представлен абсолютно правильно: необходимо давать первые 3-и значащие цифры. При этом не нужно учитывать первые нули числа и до, и после запятой (здесь очень часто делается ошибка).

Примеры чисел с первыми тремя значащими цифрами:

437; 30,6; 52,0 (здесь «0» тоже значащая цифра); 7,28; 3,80; 0,196; 0,0238; 0,00507; 0,0000921.

Чтобы не было сомнений (прежде всего, у преподавателя, который будет проверять ДЗ), что всегда учитываются три значащие цифры, давайте всегда в ДЗ будем ставить нули в младших разрядах (в предыдущем абзаце числа 52,0; 3,80). Кстати, в методичках [М1], [М2] так сделано – стоят нули в младших разрядах.

4-я значащая цифра округляется до нуля по известным правилам и не рассматривается.

12) Единицы физических величин.

Единицы имеют только сами физические величины. Сюда следует также отнести:

– коэффициенты, поскольку они состоят из физических величин;

– характеристики, которые являются каким-либо соотношением физических величин (например, амплитудная частотная характеристика (АЧХ), которая является отношением амплитуд входной и выходной гармоник при различных частотах).

Более никакие другие элементы математического описания процессов единиц не имеют (в нашем случае это: передаточные функции (ПФ), частотные ПФ, проекции годографов (U и V) и т. д.).

• оператор 1/p (оператор интегрирования), входящий в некоторые передаточные функции системы, имеет единицу «c» (она в данном случае и размерность);

• оператор p (оператор дифференцирования, он же – оператор Лапласа), входящий в некоторые передаточные функции системы, имеет единицу «1/с»;

• передаточные функции и частотные передаточные функции (например, W(p) и W(j)) единиц или размерностей не имеют (полные названия: "единица физической величины", "размерность физической величины");

• не принято (хотя во многих случаях это было бы и возможно) проставлять единицы или размерности у вещественной и мнимой частотных характеристик (например, ВЧХ U() и МЧХ V()).

На тексте и на графиках должны быть даны единицы физических величин. Если величина не имеет единицы, то в ДЗ следует указать, что эта величина безразмерная (следует указать ее размерность как "б/р").

Обычно угол измеряется в радианах, а частота в рад/с. Радиан является дополнительной единицей СИ с размерностью равной 1, но эту единицу (т. е. рад) следует писать (по крайней мере, в ДЗ).

13) Парные графики.

Графики АЧХ и ФЧХ (а также ЛАЧХ и ЛФЧХ) являются парными графиками – это значит, что они не должны использоваться один без другого.

Кстати, если система является минимально – фазовой (см. Главу 3), то достаточно одного графика (либо АЧХ, либо ФЧХ), но «работать» с двумя графиками гораздо удобнее.

Итак, АЧХ и ФЧХ (ЛАЧХ и ЛФЧХ) парные графики – пара графиков дается обязательно на одной странице, и один под другим. Причем масштаб по оси частот  у обоих графиков должен быть одинаковым. Масштаб ЛАЧХ, который необходимо использовать в ДЗ, указан в методичке [M1].

Целесообразно эти пары графиков давать на отдельных страницах. Предлагаемые масштабы ЛАЧХ и рассчитаны как раз на это. Пары графиков АЧХ и ФЧХ также должны иметь достаточно большие масштабы и также должны строиться на отдельных страницах.

14) Начало и окончание графика ФЧХ.

Необходимо давать значения, из которого начинается график ФЧХ, и к которому он стремятся. Указывать эти значения не нужно в случаях, если нет никаких сомнений. Показать эти значения можно пунктирной линией. Сказанное касается графиков и в обычном масштабе (ФЧХ), и в логарифмическом (ЛФЧХ).

15) Представление годографов.

В ДЗ годографы имеются в пунктах 3.1, 3.2 и 10.2.

Годограф не должен быть "голым", а для этого необходимо выполнение следующих условий:

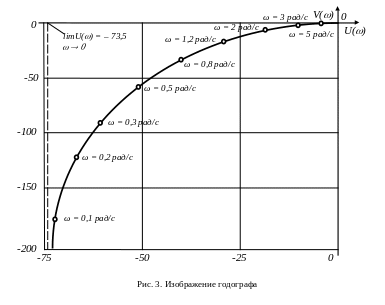
• на годографе должно быть указано несколько точек частоты  (примерно (8 – 10) точек). Точки должны быть указаны равномерно по всему годографу. Около точки необходимо указать величину и единицу частоты (см. рис. 3).

• каждой точке частоты ω_i должны соответствовать вещественная U(ω) и мнимая V(ω) частотные характеристики, которые целесообразно свести в таблицу для удобства проверки:

ω; рад/с

U()

V()

• должны четко видны начало и окончание годографа; если годограф стремится в бесконечность по одной из координат, то необходимо показать значение годографа по другой координате (например, использовать пунктирную линию, см. рис. 3).

В пунктах 3.1 и 3.2 ДЗ кривые W(j) называются просто годографами.

W(j) = U() + jV(),

где W(j) – частотная передаточная функция; U() – вещественная (действительная) частотная характеристика; V() – мнимая частотная характеристика.

А в п. 10.2 ДЗ кривая имеет следующие названия (но это тоже годограф): кривая Михайлова, характеристическая кривая, годограф вектора D(j).