Следствие

Немедленным следствием из теоремы является то, что любой многочлен степени n над полем комплексных чисел имеет в нём ровно n корней, с учётом кратности корней.

Разложение многочленов на множители

• Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)

• Пример. Разложить многочлен на множители 12 y ³ – 20 y ². Решение. Имеем: 12 y ³ – 20 y ² = 4 y ² · 3 y – 4 y ² · 5 = 4 y ² (3 y – 5). Ответ. 4 y ²(3 y – 5).

• Использование формул сокращенного умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.

• Пример. Разложить на множители многочлен x ⁴ – 1. Решение. Имеем: x ⁴ – 1 = ( x ² ) ² – 1 ² = ( x ² – 1)( x ² + 1) = ( x ² – 1 ² )( x² + 1) = ( x + 1)( x – 1)( x ² + 1). Ответ. ( x + 1)( x – 1)( x ² + 1).

• Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

• Пример. Разложить на множители многочлен x ³ – 3 x ² y – 4 xy + 12 y ². Решение. Сгруппируем слагаемые следующим образом:  x ³ – 3 x ² y – 4 xy + 12 y ² = ( x ³ – 3 x ² y ) – (4 xy – 12 y ² ). В первой группе вынесем за скобку общий множитель x ², а во второй − 4 y . Получаем:  ( x ³ – 3 x ² y ) – (4 xy – 12 y ² ) = x ² ( x – 3 y ) – 4 y ( x – 3 y ). Теперь общий множитель ( x – 3 y ) также можно вынести за скобки:  x ² ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x ² – 4 y ). Ответ. ( x – 3 y )( x ² – 4 y ).

• Способ выделения полного квадрата. Метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.

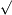• Пример. Разложить на множители многочлен x ⁴ + 4 x ² – 1. Решение. Имеем x4+4x2−1=x4+2 2x2+4−4−1=(x2+2)2−5=(x2+2− 5)(x2+2− 5)

ВИЕТА ТЕОРЕМА

о корнях - теорема, устанавливающая соотношения между корнями и коэффициентами многочлена. Пусть   - многочлен степени пс коэффициентами из нек-рого поля н старшим коэффициентом 1. Над полем, содержащим все корни   (напр., над полем разложения для  ), многочлен разлагается на линейные множители:

где   - корни   В. т. устанавливает справедливость соотношений (формулы В и е т а):

 Формулы Виета 

     Если   и   - корни многочлена (каждый кратный корень взят здесь столько раз, какова его кратность), то:

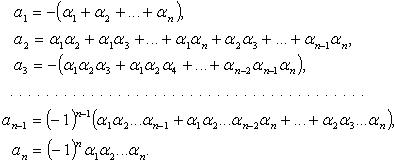
     В частности, при   при 

19) Многочлен f(x) с действительными коэффициентами 

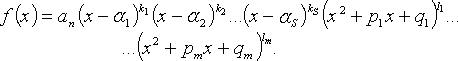
Здесь   - различные действительные корни многочлена, кратностей   соответственно   - различные пары действительных чисел, удовлетворяющих неравенствам  (каждый множитель   можно представить в виде   где   - пара сопряженных комплексных корней кратности  ).

• Теоремы о многочленах с действительными коэффициентами

20)  Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции.

      Матричная алгебра имеет обширные применения в различных отраслях знания – в математике, физике, информатике, экономике. Например, матрицы используется для решения систем алгебраических и дифференциальных уравнений, нахождения значений физических величин в квантовой теории, шифрования сообщений в Интернете.

      Матрица обозначается одной из заглавных букв латинского алфавита, а набор ее элементов помещается в круглые скобки:

(1)

      Представленная формулой (1) матрица A имеет m строк и n столбцов и называется  m×n  матрицей (“эм на эн матрицей”) или матрицей размера  m×n. Строки матрицы нумеруются сверху вниз, а столбцы – слева направо.

Матричный элемент, расположенный на пересечении i-ой строки и j-го столбца, называется i,j-м элементом и записывается в виде  a_i j , а выражение  A = || a_i j ||  означает, что матрица Aсоставлена из элементов  a_i j .

      Матрица     размера  1×n  называется строчной или вектор-строкой.

      Матрица     размера  n×1  называется столбцевой или вектор-столбцом. Для краткости вектор-строку и вектор-столбец обычно называют просто векторами.

      Особую роль играют матрицы, у которых число строк совпадает с числом столбцов, то есть матрицы размера  n×n. Такие матрицы называются квадратными При ссылке на квадратную матрицу достаточно указать ее порядок. Например, матрица третьего порядка имеет размер  3×3.

      Квадратная матрица порядка 1 отождествляется с единственным ее элементом.

• Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.

• Диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

• Транспонированная матрица - это матрица, полученная из исходной путем замены строк на столбцы. Например,

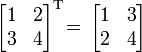
или вот так

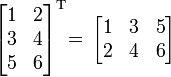
• Сложение матриц 

     Суммой матриц   и   одинаковых размеров называется матрица   тех же размеров, у которой  Обозначение: C = А + В.

     Свойства сложения матриц: А + В = В + А, (А + В) + С = A + (B + C), А + 0 = A, А + (-A) = 0,   A, B, C.

• Вычитание матриц 

А - В = А + (-В).

•  Умножение матрицы на число \

Каждый элемент матрицы надо умножить на это число.

Свойства умножения матриц на число.

   ,       и 

20