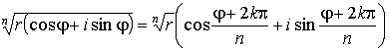11) Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0

Коэффициенты уравнения – действительные числа, но по крайней мере одно из чисел А, И или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка.

Эллипсом ( рис.1 ) это геометрическое место точек на плоскости, сумма расстояний от которых до 2 ух данных точек называемых фокусами есть величина постоянная

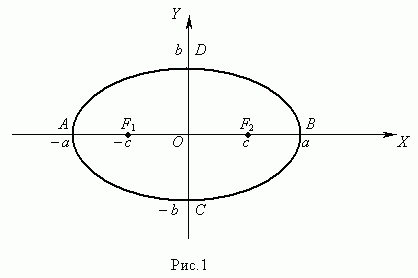
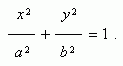
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При  a > b фокусы эллипса лежат на оси ОХ  ( рис.1 ) , при  a < b  фокусы эллипса лежат на оси ОY , а при  a = b  эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом,  окружность есть частный случай эллипса.

Отрезок  F₁F₂ = 2 с ,  где  , называется фокусным расстоянием. Отрезок  AB = 2 a называется большой осью эллипса, а отрезок  CD = 2 b –малой осью эллипса. Число  e = c / a ,  e < 1 называется эксцентриситетом эллипса.

 

Пусть  Р ( х₁ ,  у ₁ ) – точка эллипса, тогда  уравнение касательной к эллипсу в данной точке имеет вид:

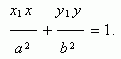
Условие касания прямой  y = m x + k  и эллипса  х ² / a ²  +  у  ² / b ²  = 1 :

 

 

k ²  = m ² a ² + b ² .

Гиперболой называется геометрическое место точек на плоскости, модуль разности расстояний которых до 2-ух данных точек называется фокусами, есть величина постоянна.

Пусть дана гипербола. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид

 (1)

где  . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. Вершины гиперболы суть точки А’ и А.

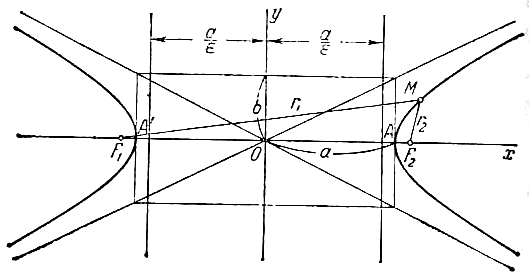
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.

Отрезки длиной 2a и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженного) являются асимптотами гиперболы, их уравнения суть

, 

Уравнение

 (2)

определяет гиперболу, симметричную относительно координатных осей, с фокусами на оси ординат; уравнение (2), как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.

Две гиперболы, которые определяются уравнениями

, 

в одной и той же системе координат, называются сопряженными.

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

 (1)

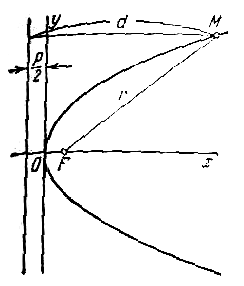
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

Фокальный радиус произвольной точки М(x; y) параболы (то есть длина отрезка F(M) может быть вычислен по формуле

.

Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат - с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

 (2)

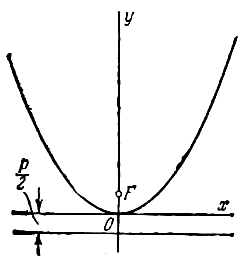
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

 (3)

если она лежит в верхней полуплоскости (рис.), и

 

 (4)

если в нижней полуплоскости (рис.)

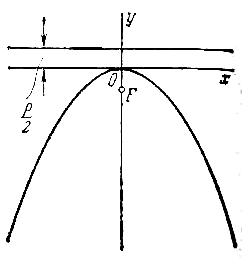
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Окружность это геометрическое место точек на плоскости равноудаленных от данной точки называемой центром.

 (x – a)² + (y – b)² = R², где a и b – координаты центра A окружности ω (A; R) 

12) Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О₁ есть геометрическое место всех точек пространства, находящихся от точки O₁ на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками простран­ства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего ко­ординаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменны­ми х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называ­ются текущими координатами точек поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M₁(x₁;y₁;z₁) на данной поверхности, достаточно подставить координаты точки M₁ в уравнение поверхности вместо пере­менных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.

Уравнение плоскости, проходящей через данную точку M(x₀, y₀, z₀) перпендикулярно данному вектору 

→

n

 = {A, B, C} имеет вид

A (x − x0) + B (y − y0) + C (z − z0) = 0.

• Общее уравнение (полное) плоскости

где   и   — постоянные, причём   и   одновременно не равны нулю; в векторной форме

• Уравнение плоскости в отрезках 

• Уравнение плоскости, проходящей через три заданные точки 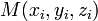 , не лежащие на одной прямой:

(смешанное произведение векторов), иначе

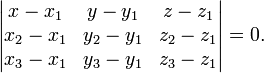
• Нормальное (нормированное) уравнение плоскости

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Две плоскости в пространстве могут быть либо параллельны, в частном случае совпадать друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют  собой частный случай пересекающихся плоскостей.

1) если  , то плоскости совпадают;

2) если  , то плоскости параллельны;

3)  если   или  , то плоскости пересекаются и система уравнений

                                                   (6)

является уравнениями прямой пересечения данных плоскостей.

13)Положение прямой в пространстве вполне определено, если задать какую-либо точку Мо на прямой и вектор S, параллельный этой прямой.

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные Aи B не равны нулю одновременно. Вектор с координатами (A,B)называется нормальным вектором и он перпендикулярен прямой. 

• Параметрические уравнения прямой могут быть записаны в виде:

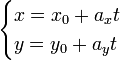
где t — производный параметр, a_x, a_y — координаты x и y направляющего вектора прямой.

• Каноническое уравнение прямой в пространстве

• Векторно-параметрическое уравнение прямой 

• Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

– прямые совпадают.

где  — точки, принадлежащие прямым   и   соответственно, a     — направляющие векторы (рис.4.34). Обозначим через  вектор, соединяющий заданные точки.

Перечисленным выше случаям взаимного расположения прямых   и   соответствуют следующие признаки:

– прямые   и   скрещивающиеся   векторы   не компланарны;

– прямые   и   пересекаются   векторы   компланарны, а векторы   не коллинеарны;

– прямые   и   параллельные   векторы   коллинеарны, а векторы   не коллинеарны;

– прямые   и   совпадают   векторы   коллинеарны.

• Если прямая L( 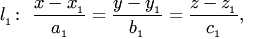) параллельна плоскости Q (Ax+By+Cz+D=0) , то векторы n(A;B;C) и S(a1;b1;c1) перпендикулярны, а потому

S*n=0, т.е. Am+Bn+Cp=0 является условием параллельности прямой и плоскости.

Если прямая L перпендикулярна плоскости Q, то векторы n и S параллельны. Поэтому неравенства A/m=B/n=C/p являются условиями перпендикулярности прямой и плоскости.

14) Комплексные числа это выражения вида z=x+iy , где x R, y R, i- мнимая единица удовлетворяющая условию i^2=-1.

• Запись комплексного числа z в виде x + iy, 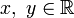 , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i² = − 1):

(a + ib) + (c + id) = (a + c) + i(b + d);

• Тригонометрическая и показательная формы

Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент   (x = rcos φ, y = rsin φ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме

z = r(cos φ + isin φ).

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

z = re^iφ,

где e^iφ — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

• Умножение комплексного числа

Z1*Z2=X1X2-Y1*Y2+i(X1Y2+X2Y1) алгебраическая форма

Z1*Z2=R1R2(cos(fi1+fi2)+isin(fi1+fi2)) тригонометрическая форма(14.1)

• Деление комплексного числа

Деление комплексного числа a + bi на комплексное число c + di  0 определяется как операция обратная умножению и выполняется по формуле:

. Алгебраическая форма

Z1/Z2=R1/R2(cos(fi1-fi2)+isin(fi1-fi2)) тригонометрическая форма

• Комплексное сопряжение — операция над комплексным числом (набором комплексных чисел, оператором), при которой вещественная часть остаётся постоянной, а мнимая — меняет знак. Комплексное число z₂, сопряженное заданному комплексному числу z₁, выражается покомпонентно как:

если  ,

то 

Операция комплексного сопряжения обладает следующими легко проверяемыми свойствами:

		(1)
		(2)
		(3)
		(4)

• 15)Возведение в степень комплексное число

Теорема: Если z=r(cos(fi)+isin(fi)) то zⁿ = rⁿ(cos n + i sin n) (14.3) –формула муавра

Доказательство 1)Если n N то формула (14.4) следует из (14.1)

2)Если n=0 z^0=r^0(cos0+isin))=1

3)n<0 Пусть m=-n; m N

zⁿ =1/ z^m =1/( r^m)(cosm(fi)+isinm(fi))=

rⁿ *(cosm(fi)-isinm(fi))= rⁿ (cos(-m(fi))+isin(- m(fi))= rⁿ (cosn(fi)+isinn(fi)) ч.т.д.

• Извлечение корня из комплексного числа

Корнем n-й степени из комплексного числа называется такое комплексное число, n-я степень которого равна подкоренному числу.  Таким образом, равенство:

равносильно равенству

ρn(cos nψ + i sin nψ) = r (cos φ + i sin φ)

Но у равных комплексных чисел модули должны быть равны, и аргументы могут отличаться лишь кратным 2p, т.е.

ρn = r,     nψ = φ + 2kπ,

откуда

где  есть арифметическое значение корня и k – любое целое число. Таким образом мы получаем:

(16)

т.е. для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня. В формуле (16) число k может принимать всевозможные целые значения; однако можно показать, что различных значений корня будет только n, и они будут соответствовать значениям:

k = 0, 1, 2, …, (n-1)

(17)

Чтобы доказать это, заметим, что правые части в формуле (16) будут различными при двух различных значениях k = k1 и k = k2 тогда, когда аргументы  и  отличаются не кратным 2π, и будут одинаковыми, если указанные аргументы отличаются кратным 2π. Но разность (k1 – k2) двух чисел из ряда (17) по абсолютному значению меньше n, а потому разность

не может быть кратна 2π, т.е. n значениям k из ряда (17) соответствуют n различных значений корня. Пусть теперь k2 – целое число (положительное или отрицательное), не заключающееся в ряде (17). Мы можем представить его в виде:

k2 = qn + k1

где q – целое число и k1 – любое число из ряда (17), а потому

,

т.е. значению k2 соответствует то же значение корня, что и значению k1, заключающемуся в ряде (17). Итак, корень n-й степени из комплексного числа имеет n различных значений. Исключение из этого правила представляет лишь частный случай, когда подкоренное число равно нулю, т.е. r = 0. В этом случае все указанные выше значения корня равны нулю.

16) Многочлен – сумма одночленов.

многочленом n-ой степени называется функция вида

где - коэффициенты;   - старший коэффициент;