Примеры решения задач контрольной работе № 1
Пример 1. Решить систему линейных уравнений по формулам Крамера
Решение.
Вычислим определитель системы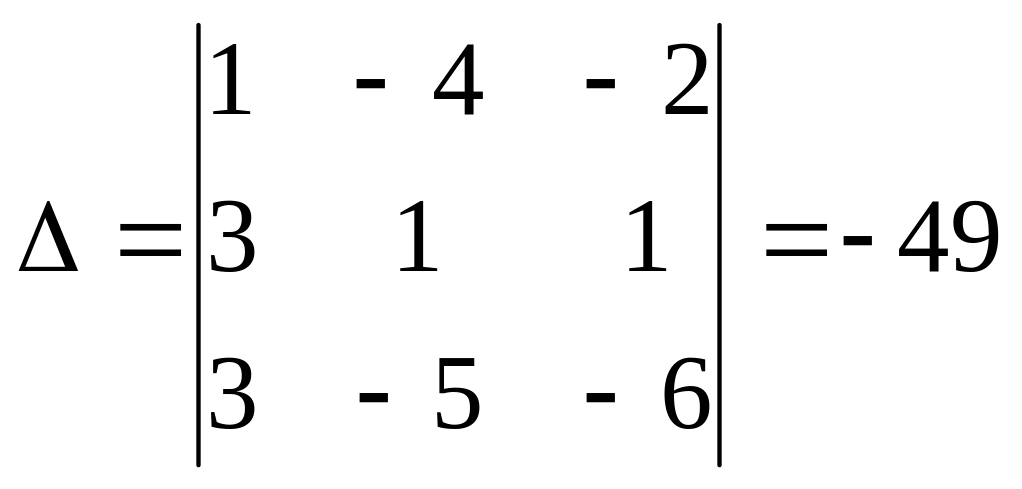 
.
Определитель отличен от нуля. Следовательно, система имеет единственное решение
Решая систему уравнений методом Крамера, вычислим дополнительные определители:
По формулам Крамера
получим решение системы уравнений:
Пример 2. Решить систему уравнений методом Гаусса.
Решение. В соответствие с методом Гаусса запишем расширенную матрицу, состоящую из коэффициентов при неизвестных и столбца свободных членов
С помощью элементарных преобразований из расширенной матрицы системы получим треугольную матрицу. Умножим первую строку на 2 и прибавим ее ко второй. Умножим первую строку на 1 и прибавим ее к третьей. Умножим первую строку на 3 и прибавим ее к четвертой. Получим
.
Поменяем местами вторую и третью строки. Четвертую строку разделим на 4. Получим
Умножив полученную вторую строку на 3, прибавим ее к третьей строке; прибавим вторую строку к четвертой . Получим
Таким образом, основная матрица приведена к «треугольному виду». Система имеет единственное решение.
Запишем систему в явном виде
Осуществляя обратный ход от последнего уравнения к первому, получаем решение системы:
Пример 3. Решить систему уравнений методом Гаусса.
Решение. Запишем расширенную матрицу системы
Умножим первую строку на 1 и прибавим ее к третьей. Умножим первую строку на 2 и прибавим ее к четвертой. Получим
.
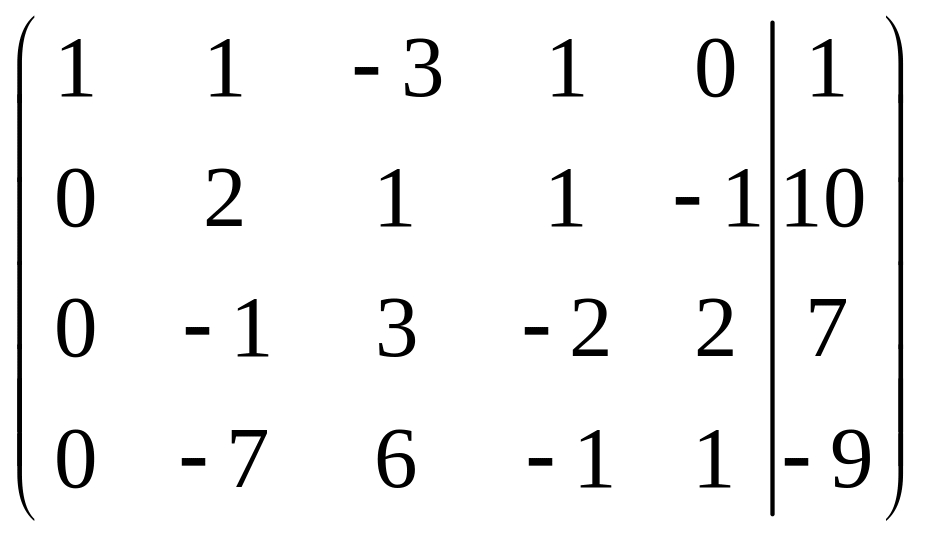Поменяем местами вторую и третью строки. Получим
Умножив полученную вторую строку на 2, прибавим ее к третьей строке; умножим вторую строку на −7 и прибавим к четвертой
Умножим третью строку на 15, а четвертую на 7. Затем прибавим третью строку к четвертой
Таким образом, матрица приведена к «виду трапеции». Система имеет бесчисленное множество решений.
Запишем систему в явном виде
Пусть
.
Осуществляя обратный ход от последнего
уравнения к первому, получаем решение
системы:
Пример 4.
Даны координаты
вершин пирамиды
:
Найти:
1) длину ребра
;
2) угол между ребрами
и
;
3) уравнение ребра
,
уравнение плоскости
и угол между ребром
и плоскостью
;
4) уравнение высоты
, опущенной из вершины
на грань
и ее длину;
5) площадь грани и объем пирамиды;
6) показать, что
векторы
,
,
образуют базис и найти координаты
вектора
в этом базисе.
Решение.
Найдем координаты векторов, которые
совпадают с выходящими из вершины
ребрами пирамиды:
1) Длина ребра
совпадает с расстоянием между
точками
и
:
2) Определим угол
между векторами, используя скалярное
произведение. Так как
то
и
3) Уравнение прямой,
проходящей через две точки, имеет вид
Подставляя в уравнение координаты точек
A1 и A4 , получим
Уравнение плоскости,
проходящей через три заданные точки,
имеет вид
Подставляя в уравнение координаты точек
,
и
,
получим
Синус угла между прямой
и плоскостью
определяется по формуле
Используя эту формулу, находим
4) Уравнение высоты
найдем как уравнение прямой, проходящей
через точку
перпендикулярно плоскости
,
задаваемой уравнением
.
В качестве направляющего вектора прямой
может быть взят вектор нормали плоскости
.
Уравнение высоты имеет вид
Для нахождения
длины высоты можно использовать формулу
Объем V и площадь
будут найдены в п. 5). Поэтому
5) Площадь треугольника
равна половине площади параллелограмма,
построенного на векторах
и
.
Найдем вначале векторное произведение
этих векторов. Имеем
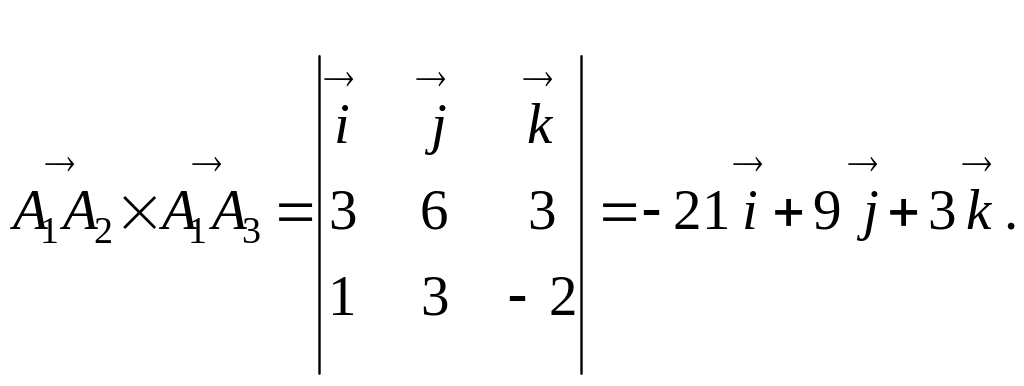Следовательно,
(кв. ед.). Объем пирамиды равен
части объема параллелепипеда, построенного
на данных векторах, поэтому вначале
находим смешанное произведение этих
векторов. Имеем
Поэтому
.
6) Для того, чтобы
векторы
,
,
образовывали базис необходимо и
достаточно, чтобы их смешанное произведение
было отлично от нуля. В п. 5) мы уже
вычислили смешанное произведение
a = 18 0.
Таким образом эти
векторы образуют базис. Найдем координаты
вектора
в базисеa,
,
.
Обозначим эти координаты x, y, z . Тогда
имеем равенство
=
xa + y
+
z
,
которое в координатной форме примет
вид системы уравнений относительно
неизвестных x, y, z
.
Решим систему
уравнений методом Крамера. Определитель
этой системы
=
18.
Вспомогательные определители:
,
,
.
Решение системы уравнений получим по формулам Крамера
Итак, вектор в базисе a , , имеет координаты ( 1,1,0).
Пример 5.
Даны координаты вершин треугольника
:
,
,
.
Найти:
1) уравнения сторон и их угловые коэффициенты;
2) угол в радианах или градусах с точностью до двух знаков;
3) уравнение высоты и ее длину;
4) уравнение медианы и координаты точки пересечения этой медианы с высотой .
Сделать чертеж.
Решение.
Найдем координаты векторов
и
.
1) Уравнение стороны
получим как уравнение прямой, проходящей
через две заданные точки
.
Подставляя в уравнение координаты точек
A и В, имеем
,
или
.
Угловой коэффициент прямой
равен
.
Аналогичным образом находим уравнение
стороны
:
,
или
.
Угловой коэффициент прямой
равен
.
2) Определим угол
между векторами
и
.,
используя скалярное произведение. Так
как
то
или
рад.
3) Уравнение высоты
находится как уравнение прямой, проходящей
через точку
перпендикулярно вектору
.
Имеем
или
.
Длина высоты
вычисляется как расстояние от точки
до прямой
:
.
4) Для нахождения
уравнения медианы
находим координаты середины отрезка
:
,
.
Уравнение медианы
получается как уравнение прямой линии,
проходящей через две точки
и
.
Имеем
или
.
Координаты точки пересечения прямых и находятся из системы уравнений этих прямых
Вычисления дают
,
.
Пример 5 Составить уравнение линии, каждая точка которой одинаково удалена от прямой х = 2 и от точки А(4,0). Сделать чертеж.
Решение.
Пусть точка М( х,у ) принадлежит
искомой линии. Расстояние между точками
и
вычисляется по формуле
.
По условию задачи
Расстояние от
точки
до прямой, заданной уравнением
,
вычисляется по формуле
.
Уравнение прямой х – 2 =0. Следовательно
.
По условию задачи d=
.
.
Возведем обе части
уравнения в квадрат. Приводя подобные,
получим
или
.
Следовательно, искомая линия является
параболой.
Пример 6. Найти пределы, не пользуясь правилом Лопиталя:
а)
;
б)
;
в)
;
г)
.
Решение.
а) Знаменатель и числитель дроби стремятся
к бесконечности при
.
Имеем неопределенность вида
.
Разделив числитель и знаменатель на x
в наибольшей степени, т.е. на x4,
получим
5,
т.к. при
каждое из слагаемых в числителе и
знаменателе кроме констант 5 и 1 стремится
к нулю.
б) Для раскрытия
неопределенности
при наличии иррациональной бесконечно
малой величины в числителе необходимо
избавиться от иррациональности, умножив
числитель и знаменатель на сопряженное
выражение, и сократить одинаковые
бесконечно малые величины.
0.
в) Воспользовавшись
формулой тригонометрии
и первым замечательным пределом
, имеем
г) Для раскрытия
неопределенности
преобразуем дробь и показатель степени
так, чтобы воспользоваться вторым
замечательным пределом.
=
=
=
=
=
=
Пример 7. Найти производные функций:
а)
;
б)
;
в)
;
г)
;
д)
.
Решение. а) Пользуясь правилом дифференцирования сложной функции и таблицей производных, имеем
.
б) Имеем
в) Имеем
г) Прологарифмируем
равенство
.
Имеем
.
Продифференцируем
обе части по
:
,
.
В результате имеем
.
д) Уравнение определяет у как неявную функцию от х. Дифференцируя обе части уравнения по х и учитывая, что у есть функция переменной х, получаем
Из этого уравнения находим
е)Найти
производную
от
функции, заданной параметрически.
. Если функция задана параметрически
то производные
вычисляется по формуле
Найдем частные производные
Имеем
