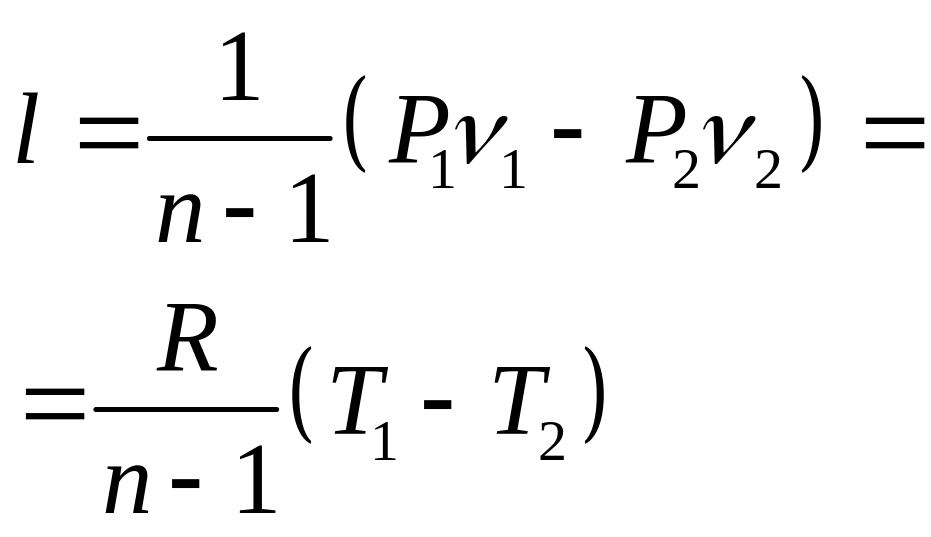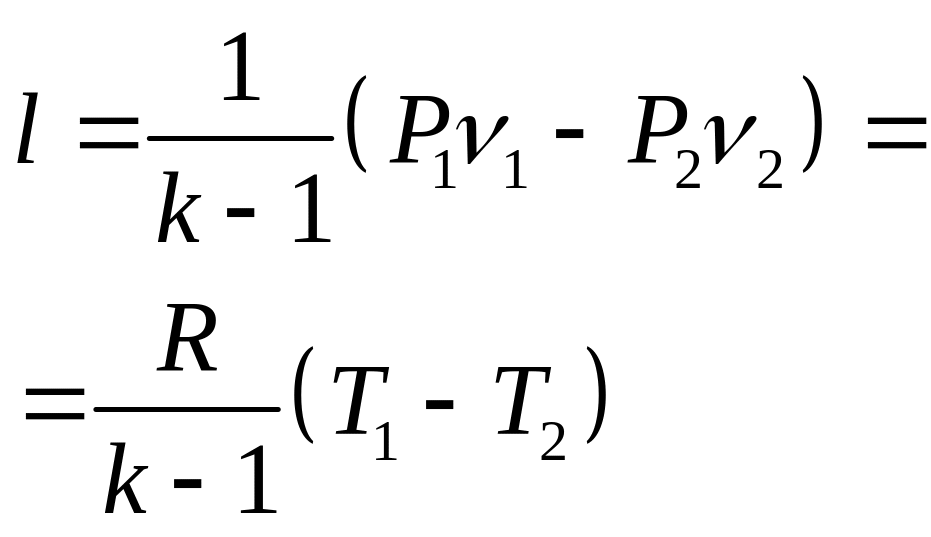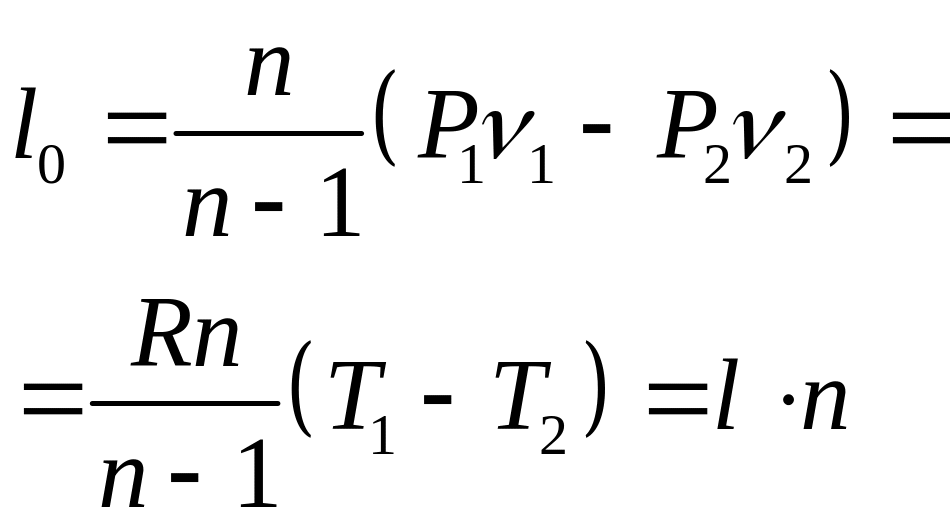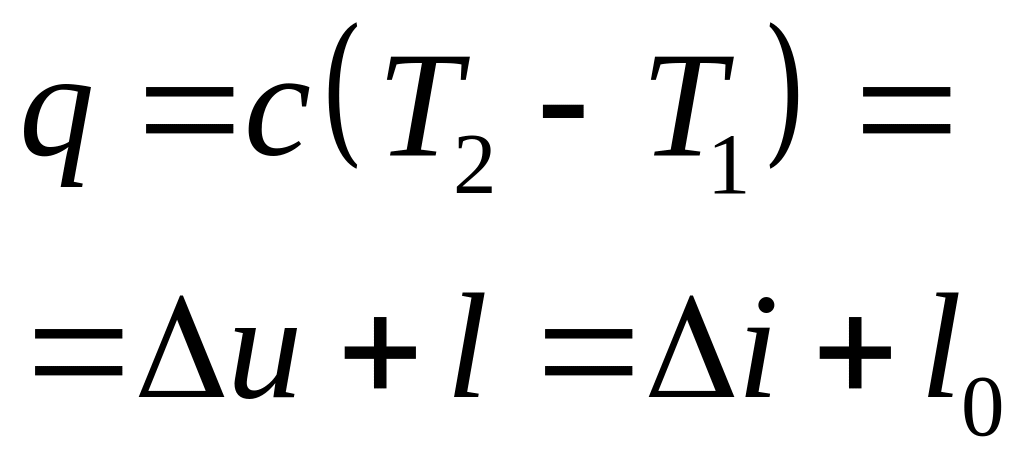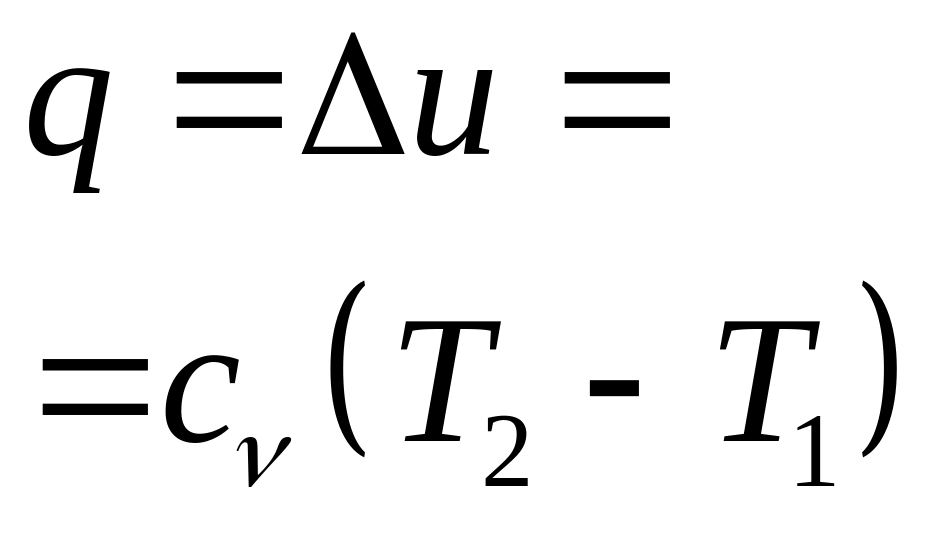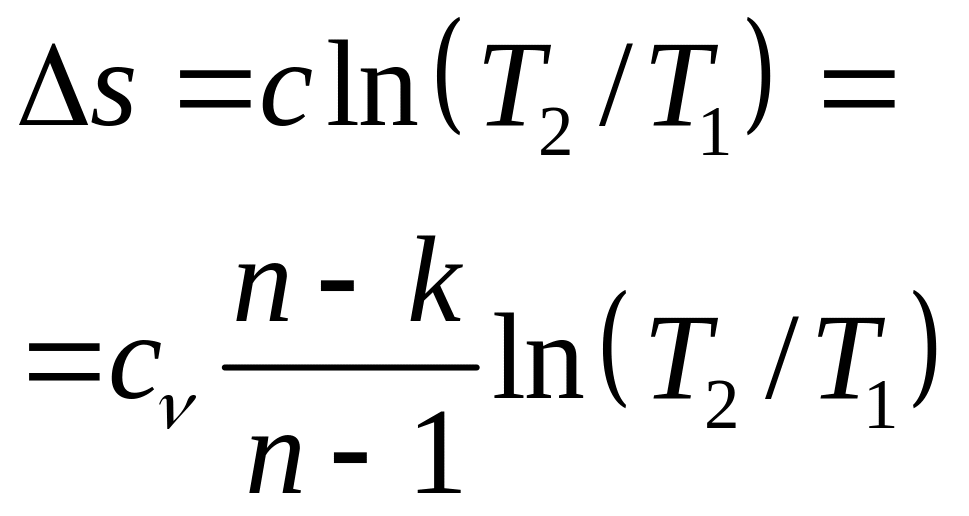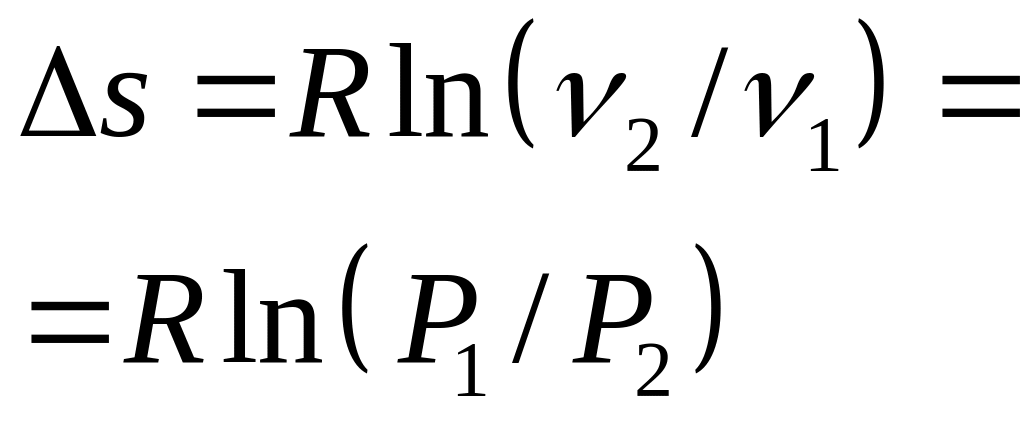- •Содержание
- •Введение
- •Часть I. Примеры решения задач по термодинамике
- •1. Система единиц измерения
- •Уравнение состояния идеального газа
- •Теплоемкость
- •4. Термодинамические процессы изменения состояния идеального газа
- •Теплота, работа, внутренняя энергия, энтальпия, I закон термодинамики
- •6. Энтропия, II закон термодинамики, цикл карно
- •Истечение газов и паров из резервуара
- •8. Смеси идеальных газов
- •9. Водяной пар, процессы, таблицы свойств воды, влажного и перегретого пара, диаграмма
- •10. Сжатие газа в компрессоре
- •11. Расширение газа в турбине
- •12. Дросселирование газов и паров
- •13. Паросиловой цикл ренкина
- •14. Эксергия, эксергетический анализ, эксергетический кпд
- •15. Влажный воздух
- •16. Холодильные машины
- •17. Циклы тепловых двигателей
- •Часть II. Задачи для самостоятельного решения
- •Литература
- •Березин Сергей Романович практикум по термодинамике учебное пособие
- •4 50000, Уфа-центр, ул.К.Маркса, 12
4. Термодинамические процессы изменения состояния идеального газа
Рассматриваются следующие обратимые термодинамические процессы: изобарный, изохорный, изотермический, адиабатический и, как обобщающий процесс – политропический.
Соотношения термодинамических параметров для каждого процесса представлены в табл. 4.1.
Таблица 4.1.
Параметры процессы
|
политропный |
изобарный |
изохорный |
изотермический |
адиабатический |
постоянные параметры процесса
|
|
|
|
|
|
показатель политропы
|
|
|
|
|
|
уравнение процесса |
|
|
|
|
|
механическая (деформационная) работа l
|
|
|
|
|
|
располагаемая
(техническая) работа
|
|
|
|
|
|
Параметры процессы
|
политропный |
изобарный |
изохорный |
изотермический |
адиабатический |
изменение
внутренней энергии
|
|
|
|
|
|
изменение
энтальпии
|
|
|
|
|
|
теплоемкость с
|
|
|
|
|
|
количество
теплоты
|
|
|
|
|
|
изменение энтропии
|
|
|
|
|
|
изменение эксергии
|
|
|
|
|
|
Задача 4.1.
Начальное
состояние 1 кг азота
![]() ;
;
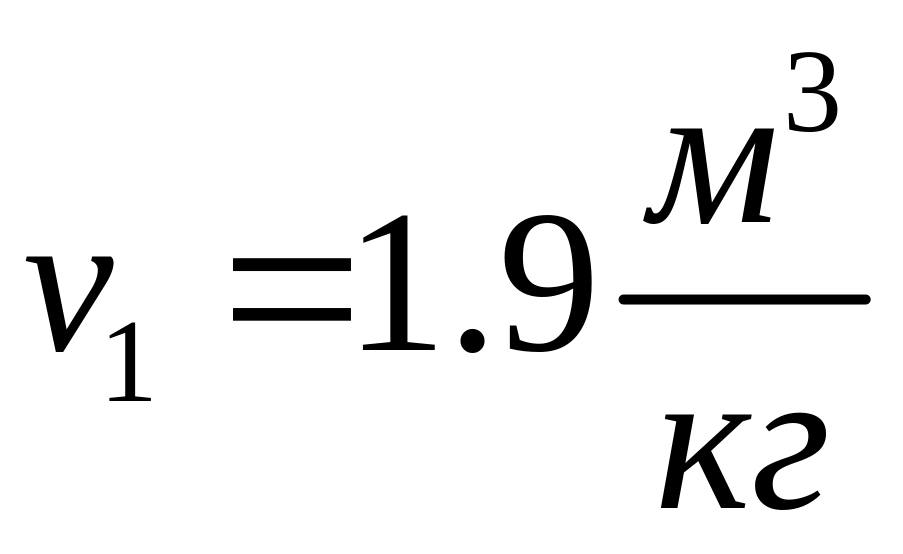 .
Нагрев при
до
.
Нагрев при
до
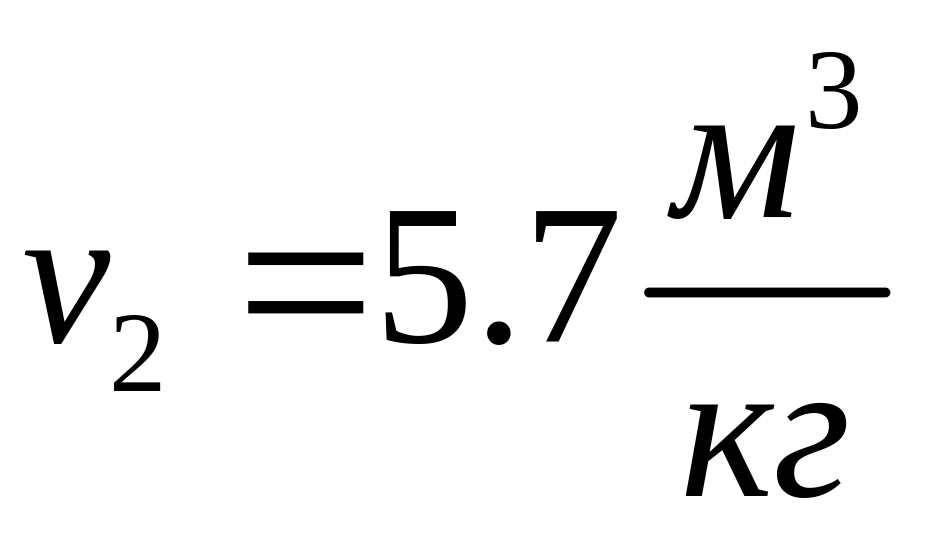 .
Найти конечную температуру, увеличение
энтальпии
и подведенную теплоту
.
Найти конечную температуру, увеличение
энтальпии
и подведенную теплоту
![]() .
Теплоемкость
газа считать постоянной.
.
Теплоемкость
газа считать постоянной.
Решение. Для
изобарного процесса имеем:
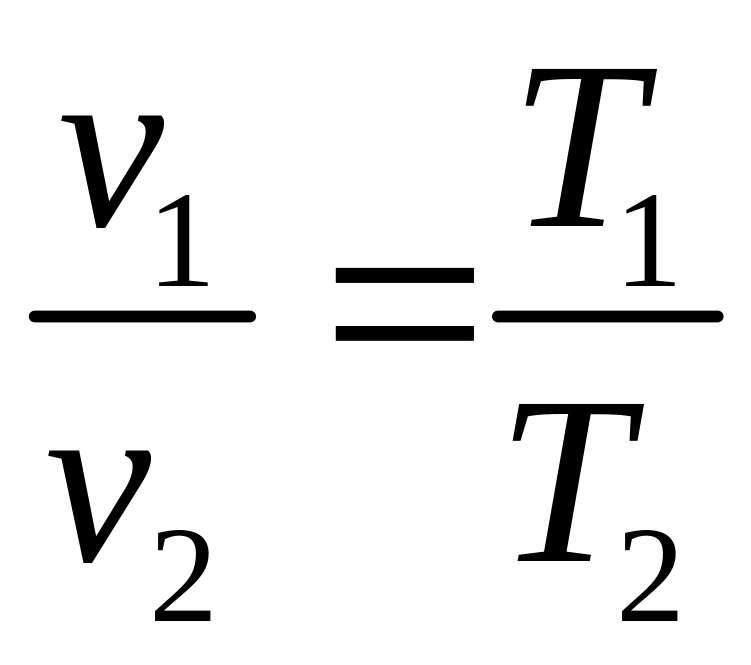 ,
тогда
,
тогда
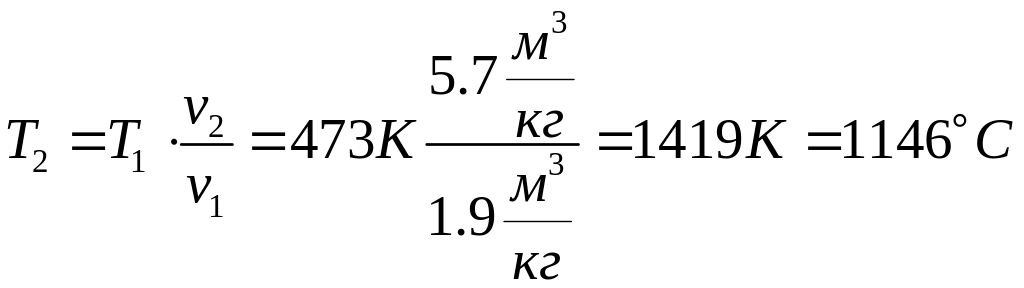 ;
;
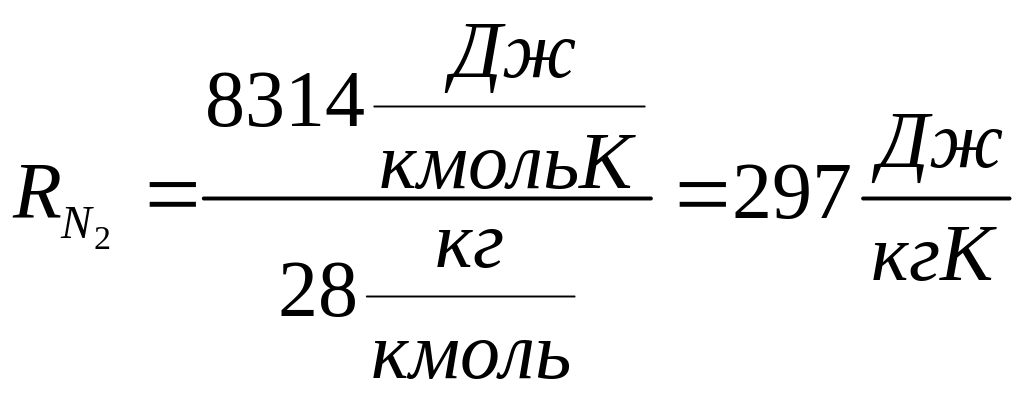 ;
;
Азот является
двухатомным газом, поэтому
![]() .
.
 .
.
I
закон термодинамики:
![]() .
.
В изобарном
процессе
и
![]() ,
тогда
,
тогда
![]() .
Таким образом, в изобарном процессе
подведенная теплота полностью расходуется
на повышение энтальпии, т.е.
.
Таким образом, в изобарном процессе
подведенная теплота полностью расходуется
на повышение энтальпии, т.е.
![]() .
.
Задача 4.2.
Показатель
политропы процесса
![]() 1.6.
Объем газа увеличивается в 3 раза. Как
изменились давление и температура газа?
1.6.
Объем газа увеличивается в 3 раза. Как
изменились давление и температура газа?
Решение. Уравнение
политропы, связывающее
![]() и
:
и
:
![]() или
или
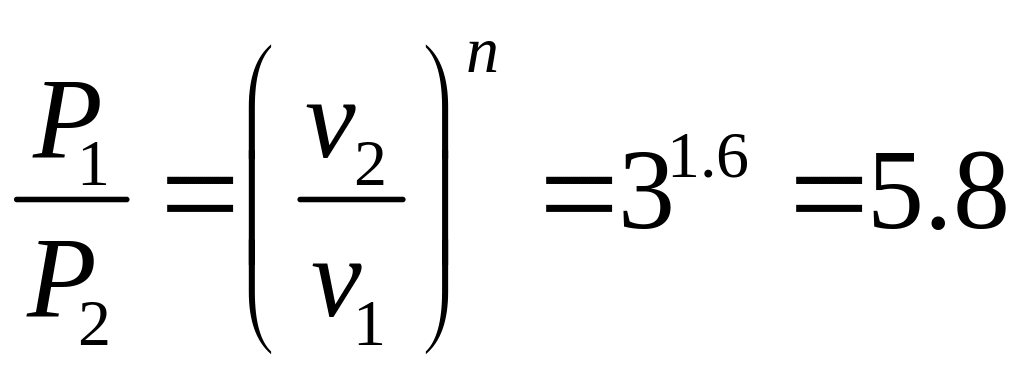 .
.
т.е. давление упало в 5.8 раза.
Уравнение политропы, связывающее и :
![]() или
или
 .
.
т.е. температура упала в 1.93 раза.
Задача 4.3.
В подогревателе
воздух нагревается при постоянном
давлении от
![]() до
до
![]() .
Какова тепловая мощность подогревателя?
Расход воздуха
.
Какова тепловая мощность подогревателя?
Расход воздуха
![]() .
.
Решение. В
рассматриваемом изобарном процессе
теплоемкость воздуха

![]() ;
;
![]()
Задача 4.4.
В поршневом
компрессоре сжимается воздух от начальных
![]() и
и
![]() .
Показатель политропы
.
Показатель политропы
![]() .
Давление в конце сжатия
.
Давление в конце сжатия
![]() .
Найти работу сжатия и количество
отведенной теплоты. Расчеты выполнить
для 1 кг газа.
.
Найти работу сжатия и количество
отведенной теплоты. Расчеты выполнить
для 1 кг газа.
Решение. Связь температуры и давления при политропическом сжатии:
 ,откуда
,откуда
 .
.
Для воздуха
![]() .
.
Располагаемая (техническая) работа сжатия:
 .
.
Знак «–» означает, что работа подводится к газу.
Теплоемкость
 .
.
Знак «–» означает, что, несмотря на рост температуры, теплота отводится от газа.
Количество отведенной теплоты:
![]() .
.
Задача 4.5.
![]() воздуха при
воздуха при
![]() изотермически сжимается, пока давление
не станет
изотермически сжимается, пока давление
не станет
![]() бар. На сжатие тратится деформационная
работа
бар. На сжатие тратится деформационная
работа
![]() .
Найти
.
Найти
![]() и
и
![]() ,
отведенную от воздуха.
,
отведенную от воздуха.
Решение.
![]() ;
;
 ,
откуда
,
откуда
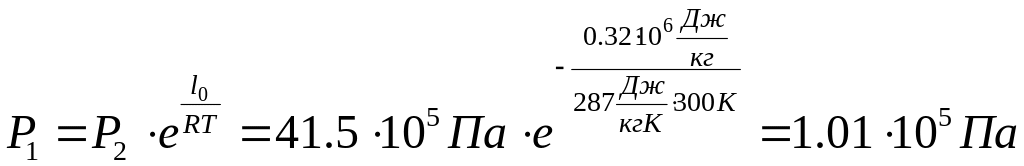 .
.
Для изотермического процесса:
![]() ,
, 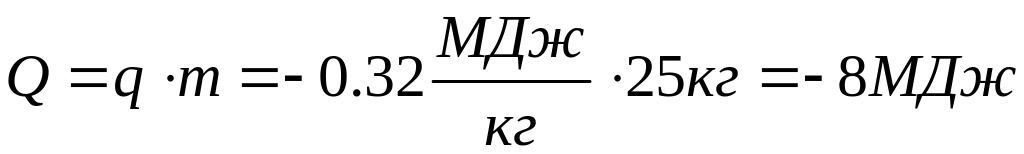 ;
;
 ;
;
 .
.