Уравнение состояния идеального газа
Уравнение Клапейрона
,
или
.
Это
уравнение записано для 1
кг
идеального газа. Умножая обе части
уравнения на молекулярный вес, выраженный
в кг
,
получим уравнение, записанное для 1
кмоля
идеального газа
,
где
– объем 1
кмоля
;
– универсальная
газовая постоянная
или
– уравнение
Менделеева-Клайперона.
Тогда
газовая постоянная
для конкретного газа находится как:
.
При
нормальных физических условиях (НФУ)
ртутного столба,
объем 1 кмоль любого газа составляет
.
Задача
2.1.
Определить
температуру газа, если при
объем 0,5 кмоля составляет
.
Решение.
Находим объем 1 кмоля при заданных условиях
.
Подставляем это значение в формулу Менделеева-Клайперона, имеем
.
Задача 2.2. Найти плотность метана при НФУ.
Решение.
,
,
.
Задача
2.3.
По
трубопроводу
подается аммиак при давлении
и температуре
.
Скорость потока
.
Найти массовый расход газа.
Решение.
,
,
,
.
Задача
2.4.
Давление
водяных паров в комнате
.
Температура воздуха
.
Объем комнаты
.
Найти массу пара.
Решение. Водяной пар при данном парциальном давлении и температуре находится в перегретом состоянии и по свойствам близок к идеальному газу.
;
;
;
.
Теплоемкость
Теплоемкостью тела называется отношение количества теплоты, подведенной или отведенной в определенном термодинамическом процессе, к изменению его температуры.
,
где
х
– параметр, сохраняющийся постоянным
в течение процесса, например
.
Данное уравнение определяет истинную
теплоемкость газа. Различают следующие
виды удельной теплоемкости:
Удельная массовая теплоемкость:
Удельная объемная теплоемкость:
;
,
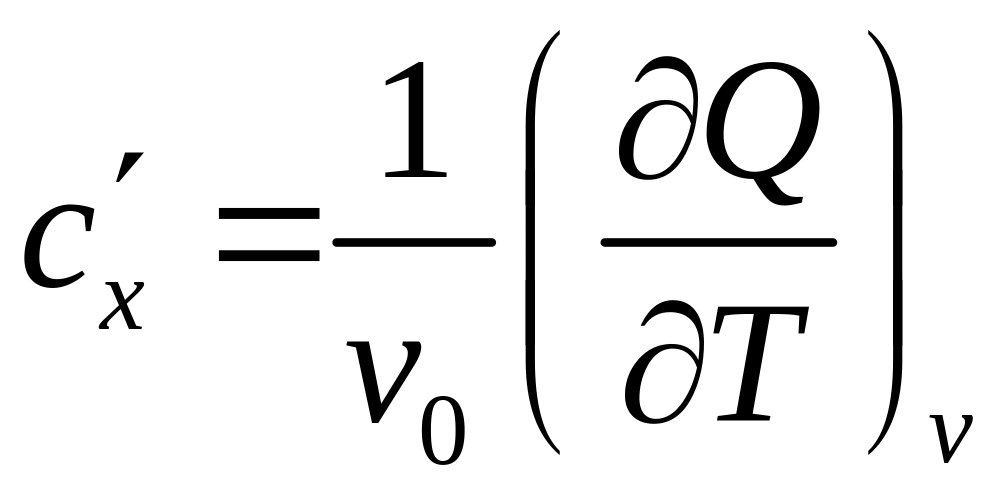где
– удельный объем при нормальных
физических условиях;
Удельная молярная теплоемкость:
,
где
– число кмолей вещества.
Теплоемкости
и
для идеального газа связаны следующими
соотношениями:
– показатель
адиабаты;
– уравнение Майера.
Из этих двух уравнений имеем для идеального газа:
;
.
Теплоемкость
в политропном процессе с показателем
политропы
.
Кроме
истинных теплоемкостей в расчетах
употребляют средние теплоемкости
,
равные отношению количества теплоты
выделившейся в конечном процессе 1-2 к
конечному изменению температуры
.
.
Здесь
учитываем, что
.
Теплоемкость (истинная и средняя) является функцией температуры. Для технических расчетов часто принимают линейную зависимость теплоемкости от температуры
.
В
таблице приведены формулы для средней
мольной теплоемкости при
для некоторых газов. Эти данные могут
быть также приведены в табличном виде.
Газ |
|
Азот |
28,97+0,002566
|
Водород |
28,78+0,001117 |
Кислород |
29,56+0,003404 |
Воздух |
28,09+0,002412 |
Водяной пар |
32,85+0,00544 |
Если
требуется найти расход теплоты для
нагрева газа от
до
,
пользуясь вышеуказанными средними
теплоемкостями, тогда определяют теплоты
и
,
необходимые для нагрева газа от
до
и от
до
.
,
.
Средняя теплоемкость в пределах от до определяется как:
.
Данные об истинной и средней теплоемкости различных газов в интервале температур приводятся в таблицах.
Задача
3.1.
В
баллоне объемом 20 л содержится воздух
при давлении
и температуре
.
Сколько нужно подвести к нему теплоты,
чтобы температура достигла
?
Теплоемкость
воздуха считать постоянной.
Решение.
Рассматривается
изохорный процесс
.
Для
воздуха:
.
Количество воздуха в баллоне:
.
Количество подведенного тепла:
.
Здесь учтено, что .
Задача
3.2.
По
экспериментальным данным молярная
теплоемкость аммиака при
,
а при
.
Определить линейную зависимость
теплоемкости от температуры.
Решение. Примем зависимость в виде:
.
Запишем эту зависимость для двух температур:
Решая совместно эти уравнения относительно А и В, получим:
.
Искомая зависимость:
.
Задача
3.3.
Воздух
в теплоизолированной трубе нагревается
электрическим током
и
на
.
Объемный расход воздуха
.
Давление 1 бар, температура воздуха на
входе
.
Найти удельную массовую теплоемкость
воздуха
.
Решение. Рассматривается подвод теплоты к потоку при . Находим массовый расход воздуха:
.
Мощность электрического нагревателя:
.
Уравнение тепловой мощности:
,
откуда
.