
- •3. Умножение матриц. Свойства.
- •4. Транспонирование матриц. Свойства.
- •5. Перестановки.
- •6. Понятие определителя.
- •7. Частные случаи определителей.
- •8. Свойства определителя.
- •9. Миноры и алгебраические дополнения.
- •10. Теоремы о разложениях определителя
- •11. Обратная матрица
- •1. Матрицы. Основные определения.
- •2. Линейные операции над матрицами и их свойства.
- •21. Понятие базиса. Координаты.
- •22. Декартова прямоугольная система координат.
- •24. Выражение для скалярного произведения в декартовых координатах.
- •23. Скалярное произведение двух векторов. Его физический смысл. Геометрические и алгебраические свойства.
- •26. Выражение для векторного произведения в декартовых координатах.
- •25. Векторное произведение. Его свойства.
- •29. Уравнение плоскости и прямой на плоскости в отрезках.
- •27. Смешанное произведение трёх векторов. Его свойства и выражение в декартовых координатах.
- •36. Гипербола и ее св-ва.
- •37. Понятие о поверхностях 2го порядка.
- •28. Общее уравнение плоскости и прямой на плоскости.
- •40. Функции и её предел.
- •35. Эллипс.
- •34.Парабола. Определение. Вывод канонического уравнения.
- •30. Нормальное ур-е пл-ти и прямой на пл-ти
- •31.Уравнения прямой, проходящей через заданную точку параллельно заданному вектору.
- •32. Канонические уравнения прямой.
- •33. Уравнение прямой на плоскости с угловым коэффициентом.
- •42.Основные теоремы о пределах
- •43.Первый замечательный предел
- •44.Второй замечательный предел
- •45.Непрерывность ф-циив точке
- •48. Некоторые свойсва непрерывной ф-ции
- •46. Классификация точек разрыва
- •50. Производная. Определение и физ. Смысл.
- •49, Сравнение бесконечно малых
- •51. Геометрический смысл производной
- •54. Обратная функция и её диффренциирование
- •55.Обратные тригонометрические функции и их производные
- •12. Ранг матрицы.
- •53. Производная сложной функции:
- •56.Производные от функций и
- •57. Гиперболические функции
- •13. Линейные системы уравнений. Основные определения. Матричная запись.
- •14. Формула Крамера
- •15. Метод Гаусса
- •16. Решение произвольных систем уравнений
- •17. Однородные системы уравнений.
- •19. Линейные операции над векторами
- •20. Линейнонезависимые системы векторов.
- •38. Действительные числа, переменные велечины
- •39. Предел переменной величины.
- •41. Бесконечно малые и бесконечно большие.Теоремы.
- •47. Непрерывность функции вна интервали и на отрезке
- •58. Таблица производных
- •52. Основные правила дифференцирования.
35. Эллипс.
Эллипсом наз. множество точек плоскости, сумма расстояния от которых до 2-ух данных точек, наз. фокусами эллипса, есть величина постоянная и большая чем расстояние между фокусами эллипса,есть величина постоянная и большая,чем расстояние между фокусами.
b
MF1+MF2=2a
можно
привести к виду : (можно
ввести обозначения),т к по определению
( a>c).
(можно
ввести обозначения),т к по определению
( a>c).
Найдём точки пересечен. эллипса с координатн. Осями.Для этого полагаем:
x=0,
 , y=±b
, y=±b
y=0,
 x=±a.
x=±a.
Величина b- наз. малой полуосью эллипса, а- большой полуосью.
с/a=E(эксцентрисетет),т к с<0, E<1.
Когда полуоси эллипса равны a=b=R

-часный случай эллипса.
34.Парабола. Определение. Вывод канонического уравнения.
П арабола
– множество всех точек плоскости,
каждая из которых одинаково удалена
от фокуса, и директрисы. Расстояние
между фокусом и директрисой называется
параметром
параболы и обозначается через р>0.
арабола
– множество всех точек плоскости,
каждая из которых одинаково удалена
от фокуса, и директрисы. Расстояние
между фокусом и директрисой называется
параметром
параболы и обозначается через р>0.
Пусть M(x;y) – произвольная
точка M с F. Проведем отрезок
MN перпендикулярно
директрисе. Согласно
определению
MF=MN.

 -каноническое
ур-е параболы
-каноническое
ур-е параболы
30. Нормальное ур-е пл-ти и прямой на пл-ти
Положение
пл-ти в пр-ве полностью определяется
расстоянием от пл-ти (р) до начала
координат и единичным вектором


Возьмем
т.М принадл
пл-ти и
принадл
пл-ти и


 проекция
вектора
на вектор
проекция
вектора
на вектор
 т.к.
вектор
т.к.
вектор
 ,то
,то



Это норм ур-е пл-ти в векторной форме.
 (1)
(1)
У

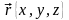 ,
а
,
а
 ,
где
,
где
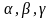 -
углы,кот он образует с корд осями
Ох,Oy,Oz
-
углы,кот он образует с корд осями
Ох,Oy,Oz
Получаем из (1)
- норм ур-е пл-ти в корд форме.
Аналогично можно вывести норм ур-е прямой на пл-ти

Норм
ур-е прямой в векторной форме будет
иметь вид в точности совпадающий с
(1).Отличия только в том, что входящие в
него векторы будут иметь по 2
координаты.Поэтому рассчитывая скалярное
пр-е получаем сл норм ур-е прямой в коорд
пл-ти:

31.Уравнения прямой, проходящей через заданную точку параллельно заданному вектору.
Полож
прямая в пр-ве полностью опр-ся некот
точкой
 принадл
прямой и вектору
принадл
прямой и вектору
 параллел
прямой.
параллел
прямой.

Пусть
 произ
точка прямой. Тогда вектор
произ
точка прямой. Тогда вектор
 лежит на прямой парал направляющему
вектору
лежит на прямой парал направляющему
вектору
 или (1)
или (1) -параметрическое
ур-е прямой в пр-ве.Число t
параметрич. При изменении параметра t
от
-параметрическое
ур-е прямой в пр-ве.Число t
параметрич. При изменении параметра t
от
 до
+
до
+ перемещается точка,определяемая
концом,радиус вектора
пробегает положение всех точек прямой.
перемещается точка,определяемая
концом,радиус вектора
пробегает положение всех точек прямой.
Предположим,что
напр вектор
 ,
тогда учитывая что
,
тогда учитывая что
 ,
,
 из ур-я (1) получаем 3 ур-я скалярных,связывающих
соотв координаты этих векторов.
Параметрическое ур-е прямой в пр-ве в
коорд форме:
из ур-я (1) получаем 3 ур-я скалярных,связывающих
соотв координаты этих векторов.
Параметрическое ур-е прямой в пр-ве в
коорд форме:

