§13. Фазовое пространство.
В методе Гамильтона рассмотрим
мерное пространство, где по осям
откладываются переменные
,
это и есть фазовое пространство. Точка
в нём – фазовая точка. Здесь каждая
точка описывает определённое динамическое
состояние системы. При движении системы,
фазовая точка описывает траекторию,
называемую фазовой траекторией.
§14. Функция Гамильтона и её свойства.
Функция Лагранжа задаётся неоднозначно, т.е.
,
где
приводят к одним и тем же уравнениям движения.
То же самое справедливо и для функции Гамильтона:
,
где
[§15.] Функция Гамильтона простейших систем.
Свободная материальная точка:
Ее потенциальная энергия равна нулю,
тогда
Получим
для данного случая:
Используем
,
тогда получим:
Система свободных материальных точек:
Замкнутая система материальных точек
,
где
4. материальных точек во внешнем поле:
5. материальных точек в стационарном внешнем поле:
- зависит только от
Отличие 5-го и 3-го случая заключается в
том, что в 5-м случае
-составляющая
во внешнем поле, она аддитивна -
;
если взаимодействие частиц с внешним
полем одинаково, то
.
6. Замкнутая система двух материальных точек:
в силу однородности и изотропности пространства можем записать:
§У. 2. Задача 3
3. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.
Решение. В декартовых координатах x, y, z:
В цилиндрических координатах r, φ, z:
В сферических координатах r, θ, φ:
§16. Интегралы движения в методе Гамильтона.
Рассмотрим полную производную функцию
обобщенных координат, обобщенных
импульсов и времени
:
Используем уравнения движения Гамильтона
:
Здесь мы ввели обозначение:
- скобки Пуассона
Если
,
то
.
В этом случае мы можем сформулировать
условие того, что функция
интеграл движения:
Чтобы
была интегралом движения, скобки Пуассона
должны обращаться в нуль.
[§17.] Скобки Пуассона и их свойства.
тождество Якоби
Докажем свойство 7:
используем свойства 5 и 6:
используем свойство 1:
используем свойство 3:
Теорема Пуассона:
Пусть
и
интегралы движения, это означает, что
и
,
тогда согласно свойству 7:
=0
Скобки Пуассона интегралов движения являются интегралом движения. Если мы знаем интегралы движения, то с помощью скобок Пуассона можно получать более удобные формы интегралов движения.
Рассмотрим частные случаи скобок Пуассона:
1.
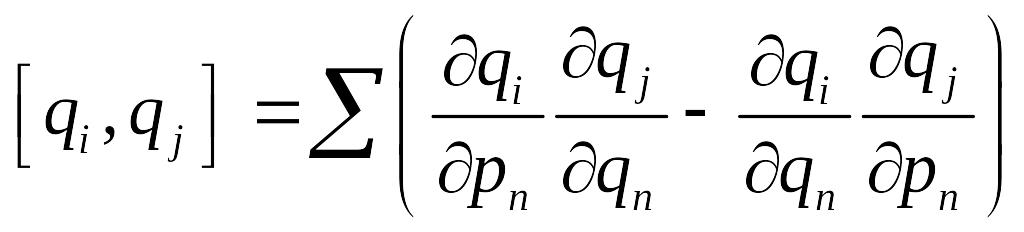
т.к.
и
,
то
2.
3.
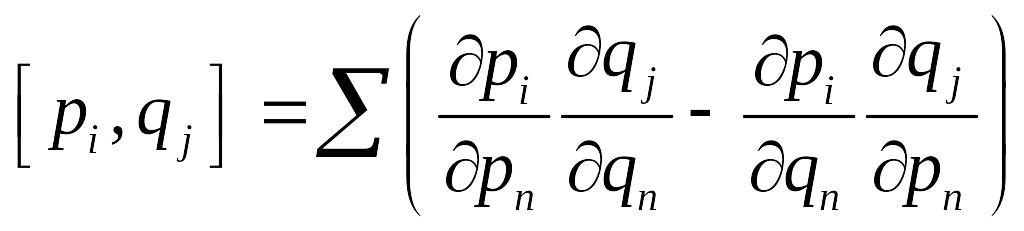
Учитывая
,
,
,
получаем:
4.
5.
6.
,
,
тогда:
7.
8.
Здесь
- компонента вектора
- функции от координат и импульсов.
,
здесь
-
скаляр.
,
здесь
- скалярная функция координат и времени.
§У. 3. Задачи4-7
4. Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса материальной частицы.
Ответ:
=-pz
=0,
=-py
5. Определить скобки Пуассона, составленные из компонент М.
Ответ:
=-Mz,
=-Mx
,
=-My.
6*. Показать, что
=0,
,
где φ – любая скалярная функция координат и импульса частицы.
Указание.
Скалярная функция может зависеть
от компонент векторов r
и p только в
комбинациях r2,p2,
.
Поэтому
и аналогично для
.
7*. Показать, что
=f
n,
где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.
Указание.
Произвольный вектор f(r,
p) может быть
написан в виде
где
-
скалярные функции