
- •1. Множества и операции над ними.
- •2. Отображения
- •3.Топологические структуры. Классификация точек множества.
- •5.Модуль и его свойства.
- •Модуль и основные неравенства.
- •1. Предел числовой последовательности.
- •2.Основные теоремы о пределах
- •3. Бмв. Теоремы о бмв
- •4. Свойства пределов выражаемые равенствами.
- •5. Свойства пределов выражаемые неравенствами
- •6.Принцип вложения отрезков. Теорема о «2х милиционерах»
- •7. Определение предела функции
- •8. Односторонние пределы функции
- •§9. Односторонние пределы. Необходимое и достаточное
- •9. Замечательные пределы
- •10. Классификация бмв. Эквиваленты.
- •11. Непрерывность функции. Теорема о приращении непрерывной функции.
- •12.Свойства непрерывных функций.
- •13. Непрерывность суперпозиции функции.
- •14. Теоремы Больцмана-Коши
- •15. Теорема Вейерштрасса
- •16. Классификация разрывов.
- •1. Производная, ее механический и геометрический смысл.
- •2. Теорема о непрерывности дифференцируемой функции.
- •3. Правила дифференцирования.
- •4. Производная сложной функции.
- •5. Производная обратной функции.
- •6. Производная элементарных функций.
- •7. Дифференциал функции. Свойства и геометрический смысл.
- •8.Инвариантность(неизменность) формы первого дифференциала.
- •9. Производные функции, заданных параметрически и неявно.
- •10. Производные и дифференциалы высших порядков.
- •11. Теоремы Ферма, Ролля, Коши и Лагранжа.
- •12. Признаки возрастания и убывания функции.
- •13. Экстремум функции. Достаточные условия.
- •14. Выпуклость функции, точки перегиба. Достаточные условия.
- •15. Асимптоты, их нахождение.
- •16. Теоремы Лопиталя.
- •17. Формула Тейлора с остаточным членов в форме Лагранжа и Пеано.
6. Производная элементарных функций.
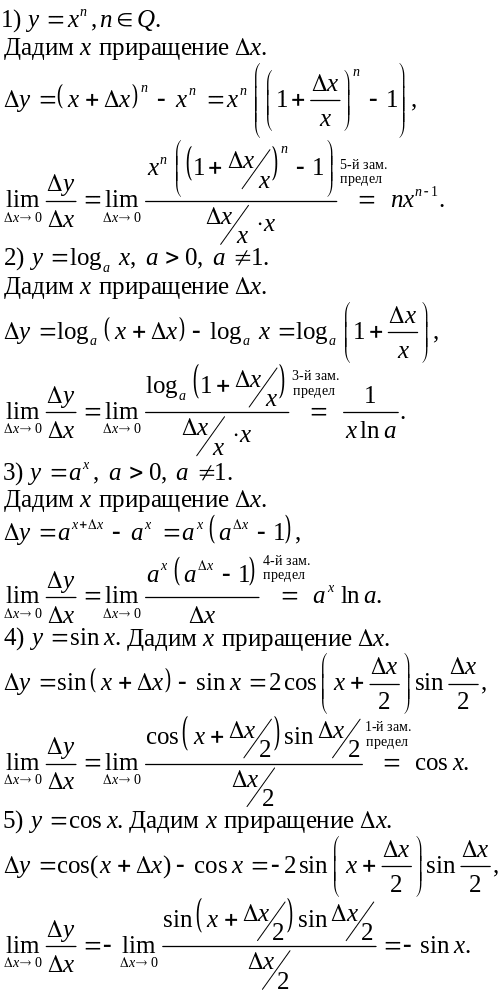
№ п/п |
Функция |
Производная |
№ п/п |
Функция |
Производная |
1. |
C – const |
|
11. |
|
|
2. |
|
|
12. |
|
|
3. |
|
|
13. |
|
|
4. |
|
|
14. |
|
|
5. |
|
|
15. |
|
|
6. |
|
|
16. |
|
|
7. |
|
|
17. |
|
|
8. |
|
|
18. |
|
|
9. |
|
|
19. |
|
|
10 |
|
|
|
|
|
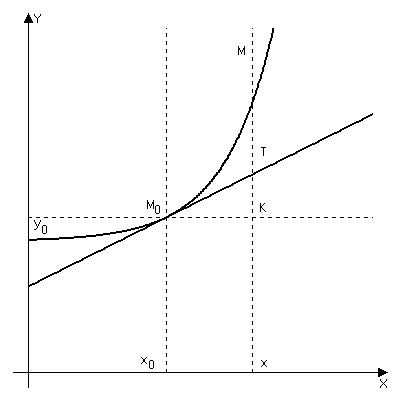
7. Дифференциал функции. Свойства и геометрический смысл.
Δf=AΔx+БМВ; AΔx=дифф. функции в данной точке.
Дифф. функции у – это приращение ординаты касательной, проведенной к графике в точке x0.
Cв-ва:
1) y=x, согл. опр.
dy=x|Δx=Δx
dx=Δx дифф. независ. аргумента – приращение этого аргумента.
df=f|dx

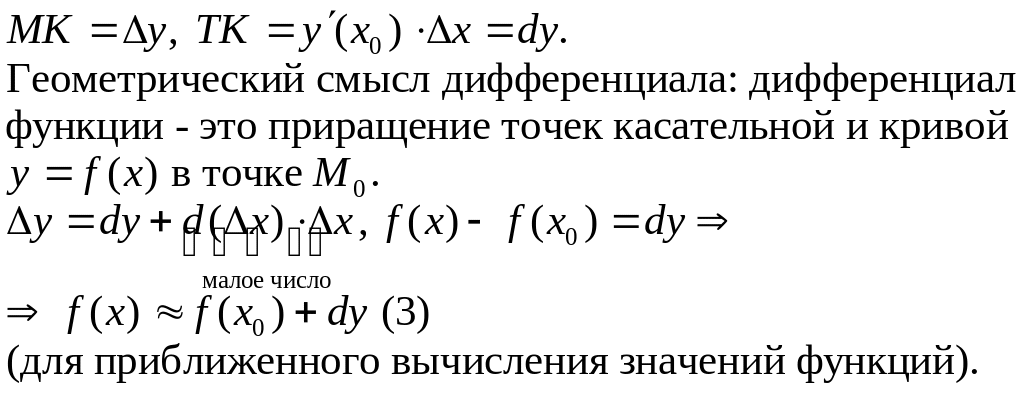
8.Инвариантность(неизменность) формы первого дифференциала.
z=z(y) y=y(x)
dz=z|ydy (3)
dz=z|xdx=z|yy|xdy=z|ydy
Св-ва:
dC=0
dCf=Сва
d(f±g)=df±dg
d(fg)=gdf+fdg
d(f/g)= gdf-fdg/g2; d(fg)=(fg)|dx=(f|g+fg|)dx=
f|dxg/df+ fg|dx/dg=df+dg
Первый дифференциал функции Z выражается по одной и той же формуле независимо от того, будет ли Z рассматриваться как функция от независимой переменной x или от зависимой переменной Y.
Форма первого дифференциала (3) сохраняется , поэтому говорят, что первый дифференциал имеет инвариантную форму или еще имеет инвариантное свойство.
9. Производные функции, заданных параметрически и неявно.
Парамеричемки:
![]()
y|x=dy/dx=y|tdt/x|tdt=y|t/x|t
y|x=y|t/x|t
пример:
![]() y|x-?
y||x-?
y|x-?
y||x-?
y|x=(t2)|/(cost)|=-2t/sint
![]()
y||x^2=(y|x)|
y||x^2=(-2t/sint)|/(cost)|==(2sint-2tcost)/(sin3t)
Неявно:
F(x,y)=0
y=y(x)
пример: xcosy+y=0 y|x-?
y=y(x)
cosy+x(-siny)y|+y|=0
y|=-cosy/1-xsiny

10. Производные и дифференциалы высших порядков.
Производная n-ого порядка – производная от производной (n-1)-ого порядка.
f ||(x) – II порядок
f |||(x) – II порядок
f |V(x) – II порядок
fV(x) – II порядок
f(n)(x)
f(n)(x)= (f(n-1)(x))|
пример:
y=arctgx
y|=1/1+x2
y||=(1/1+x2)|=-2x/(1+x2)2
Дифференциал n-ого порядка – дифференциал от (n-1)-ого порядка.
dnf(x) – обозначение
dnf(x)=d(d(n-1)f(x))
Пусть имеется f(x), x – независимый аргумент.
dnf=f(n)(x)(dx)n

