14. Теоремы Больцмана-Коши
1. Теорема о нулях непрерывной функции:
Если функция f(x) непрерывна на отрезке (a,b) и в точках а и b принимает значения разных знаков, то внутри отрезка найдется точка с, для которой f(c)=0
Док-во:
I0=[a,b]
I1=[a,b1]
I2=[a1,b1]
I0
I1
I2
f(an)≤0, an→с
f(bn)≥0, bn→с
limn→∞f(an)≤0
limn→∞f(bn)≥0 => f(c)=0
2. Теорема о промежуточном значении
Если непрерывная функция f(x) в точке а и b принимает значение f(a)=A, и f(b)=B, то функция принимает все промежуточные значения от a до b.
Док-во:
С€(A,B)
g(x)=f(x)-C
g(a)=f(a)-C=A-C<0
g(b)=f(b)-C=B-C>0
g(c)=0 => f(c)=C
15. Теорема Вейерштрасса
– об ограниченности непрерывной ф-ции.
O: Если функция f(x) определена на [a, b] и непрерывна, то она ограничена. m≤f(x)≤M
Док-во:
f(x) – не ограничена сверху, xn€[a, b]
f(xn)>n limn→∞f(xn)=∞
f(xn)>f(xn-1)
xn1 I0 I0 I1 I2
xn2 I1
xn3 I2 {xnk}
I3
– о наименьшем и наибольшем значении функции.
f(x) x0 f(x)≤ f(x0) y0=f(x0) – наиб.
x0 f(x)≥ f(x0) y0=f(x0) – наим.
O: Если непрерывн. функция f(x) задана на отрезке [a, b], то она имеет и наибольшее и наименьшее значение.
f(x)<M
=sup(точная
верхняя граница)
f(x)=
g(x)=1/(M-f(x)) 1)g(x)>0 2) g(x)-непр.
Следств: непрерывн. функция заданная на отрезке принимает все значения от наименьшего до наибольшего.
16. Классификация разрывов.
Точка x0 называется точкой разрыва функции f(x), если f(x) не определена в x0 или не является непрерывной в этой точке.
O: точка x0 называется точкой разрыва 1ого рода, если в этой точке f(x) имеет конечные, но не равные друг другу левый и правый пределы. limx→x0+0f(x)+ limx→x0-0f(x)
Для выполнения этого опр. не требуется чтоб функция была определена в x= x0, достаточно того, что она опр. слева и справа от нее. Вывод: В точке разрыва 1ого рода функция может иметь только скачок. Точка 1ого рода – устранимая точка разрыва.
O: Точка x0 называется точкой разрыва 2ого рода, если в этой точке f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из бесконечен.
1. Производная, ее механический и геометрический смысл.
St=gt2/2 St+Δt=g(t+Δt)2/2 ΔS= St+Δt- St=g/2 * (2tΔt+(Δt)2) Vcp=ΔS/Δt= g/2 * (2t+Δt)
Vмгн=limΔt→0 Vср=gt Vt=gt
limΔt→0(ΔS/Δt) – рассч. этот предел получим мгновенную скорость. Физ. смысл -> показывает скорость изменения данного процесса. Производной функции f(x) в точке x0 называется предел отношения limx→Δx((f(x)-f(x0))/x- x0)=limx→ΔxΔf/Δx
Δf=f(x)-f(x0)=f(x0+Δx)-f(x0)
Δx=x- x0
Если в данной точке имеется конечная производная, то говорят, что функция в этой точке дифференцируема. Функция называется дифференцируемой, если она дифф. в каждой точке области определения.
T: Если f(x) дифф. в точке x0, то она непрерывна в этой точке. Док-во:
f(x) f(x0)
limx→0Δf/Δx = f |(x0)
(f(x0+Δx)-f(x0))/(Δx) - f |(x0) – БМВ(Δx→0)
(f(x0+Δx)-f(x0))/(Δx) - f |(x0)=α(x)
f(x0+Δx)-f(x0)=f |(x0)Δx+α(x)Δx ф-ция непрерывна в x0
Односторонней производной функции f(x) в точке x0 называется производная справа(limΔx→0Δf/Δx=f |+(x0); Δx>0) или слева(limΔx→0Δf/Δx=f |-(x0); Δx<0).
T: Для того чтобы функция была дифф в точке x0, необходимо и достаточно, чтобы сущ. и были равны односторонние производные.
Геометр. смысл: (показать tg угла наклона)
секущей называется любая
прямая проходящая через M0
Линия предельных положений –
к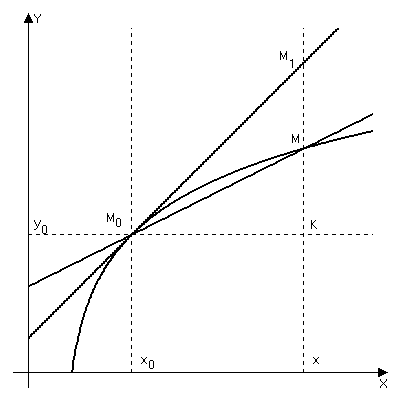
асательная
к графику в точке M0
y-y0=k(x- x0)=(Δy/Δx)(x- x0)
y-y0=y|(x0)(x- x0)
y|(x0)=tgα
