[Править] Распределение Максвелла [править] Распределение по вектору импульса

Представленное ниже очень сильно отличается от вывода, предложенного Джеймсом Клерком Максвеллом и позже описанного с меньшим количеством предположений Людвигом Больцманом.

В случае идеального газа, состоящего из не взаимодействующих атомов в основном состоянии, вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы следующим образом

,

где — квадрат вектора импульса .

Мы можем поэтому переписать уравнение (1) как:

,

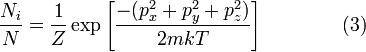где — статсумма, соответствующая знаменателю в уравнении (1), — молекулярная масса газа, — термодинамическая температура, и — постоянная Больцмана. Это распределение пропорционально функции плотности вероятности нахождения молекулы в состоянии с этими значениями компонентов импульса. Таким образом:

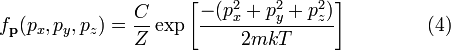
Постоянная нормировки C, определяется из условия, в соответствии с которым вероятность того, что молекулы имеют какой-либо вообще импульс, должна быть равна единице. Поэтому интеграл уравнения (4) по всем значениям и должен быть равен единице. Можно показать, что:

.

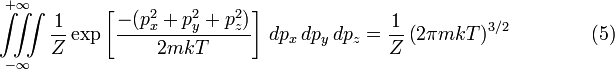Таким образом, чтобы интеграл в уравнении (4) имел значение 1 необходимо, чтобы

.

Подставляя выражение (6) в уравнение (4) и используя тот факт, что , мы получим

.

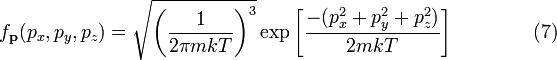[править] Распределение по вектору скорости

Учитывая, что плотность распределения по скоростям пропорциональна плотности распределения по импульсам:

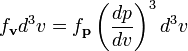
и используя мы получим:

,

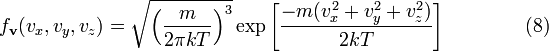что является распределением Максвелла по скоростям. Вероятность обнаружения частицы в бесконечно малом элементе около скорости равна

[править] Распределение по абсолютной величине импульса

Интегрируя, мы можем найти распределение по абсолютной величине импульса

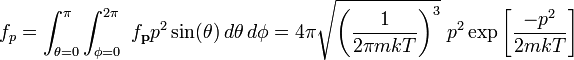
[править] Распределение по энергии

Наконец, используя соотношения и , мы получаем распределение по кинетической энергии:

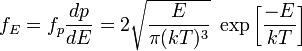
[править] Распределение по проекции скорости

Распределение Максвелла для вектора скорости — является произведением распределений для каждого из трех направлений:

,

где распределение по одному направлению:

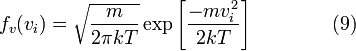
Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.

[править] Распределение по модулю скоростей

Обычно, более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, v определяется как:

поэтому модуль скорости всегда будет больше или равен нулю. Так как все распределены нормально, то будет иметь хи-квадрат распределение с тремя степенями свободы. Если — функция плотности вероятности для модуля скорости, то:

,

где

таким образом, функция плотности вероятности для модуля скорости равна

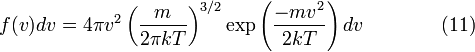
[править] Характерная скорость

Хотя Уравнение (11) дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.

[править] Наиболее вероятная скорость

наиболее вероятная скорость, — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению . Чтобы найти её, необходимо вычислить , приравнять её нулю и решить относительно :

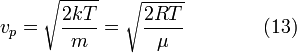
[править] Средняя скорость

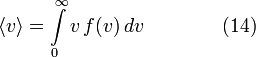
Подставляя и интегрируя, мы получим

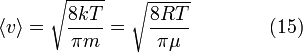
[править] Среднеквадратичная скорость

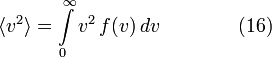
Подставляя и интегрируя, мы получим

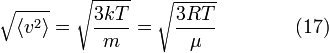
[править] Вывод распределения по Максвеллу

Получим теперь формулу распределения так, как это делал сам Джеймс Клерк Максвелл^{[источник не указан 523 дня]}. Рассмотрим пространство скоростных точек (каждую молекулу представляем как точку в системе координат ) в стационарном состоянии газа. Выберем бесконечно малый элемент объема . Так как газ стационарный, количество скоростных точек в остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функции плотности вероятности для всех направлений одинаковы.

Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента скорости молекулы не зависит от и компонент.

- фактически вероятность нахождения скоростной точки в объеме .

Правая часть не зависит от и , значит и левая от и не зависит. Но и равноправны, значит левая часть не зависит также и от . Значит, это константа.

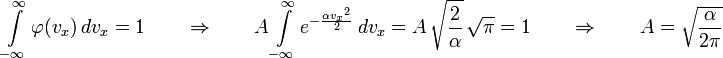
Теперь нужно сделать принципиальный шаг - ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):

где Дж/К - постоянная Больцмана.

Все направления равноправны:

Чтобы найти среднее значение , проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности:

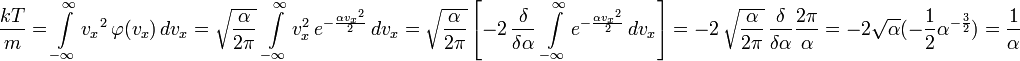
Отсюда найдём :

Функция распределения плотности вероятности для (для и аналогично):

Рассмотрим теперь распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скорости лежат в шаровом слое радиуса и толщины , и - объем этого шарового слоя.

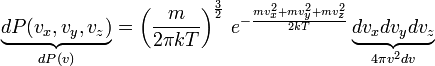
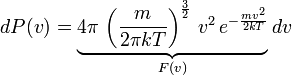
Так, мы получили - функцию плотности вероятности, которая и называется распределением Максвелла.